浙江省舟山市定海区第七中学2022年中考适应性考试数学试卷

更新时间：2022-05-12 浏览次数：125 类型：中考模拟

一、单选题

1. (2022·定海模拟) 在2，﹣3，0，﹣ $\text{[math]}$ 中最小的数是（）

A . 2 B . ﹣3 C . 0 D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·定海模拟) 已知一个几何体如图所示，则它的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·定海模拟) 对于以下四个命题：①若直角三角形的两条边长与3与4，则第三边的长是5；② $\text{[math]}$ ；③若点 $\text{[math]}$ 在第三象限，则点 $\text{[math]}$ 在第一象限；④两边及其第三边上的中线对应相等的两个三角形全等，正确的说法是（）

A . 只有①错误，其他正确 B . ①②错误，③④正确 C . ①④错误，②③正确 D . 只有④错误，其他正确

答案解析收藏纠错 + 选题
4. (2022·定海模拟) 在直角坐标系中，将直线 $\text{[math]}$ 将上平移得到直线 $\text{[math]}$ ，则直线 $\text{[math]}$ 与x轴的交点的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七下·金东期中) 如图，△ABC沿直线BC向右平移得到△DEF，已知EC=2，BF=8，则CF的长为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
6. (2022八下·台江期末) 要组织一次篮球联赛，赛制为单循环形式，每两队之间都赛一场，计划安排15场比赛.设比赛组织者应邀请x个队参赛，则x满足的关系式为（）

A . $\text{[math]}$ x（x﹣1）＝15 B . $\text{[math]}$ x（x+1）＝15 C . x（x+1）＝15 D . x（x﹣1）＝15

答案解析收藏纠错 + 选题
7. (2021八上·拱墅期中) 如图，△ABC中，点D为BC边上的一点，且BD＝BA，连结AD，BP平分∠ABC交AD于点P，连结PC，若△ABC面积为2cm² ，则△BPC的面积为（）

A . 0.5cm² B . 1cm² C . 1.5cm² D . 2cm²

答案解析收藏纠错 + 选题
8. (2022·定海模拟) 如图，正方形ABCD的顶点A、B在⊙O上，顶点C、D在⊙O内，将正方形ABCD绕点B顺时针旋转α度，使点C落在⊙O上.若正方形ABCD的边长和⊙O的半径相等，则旋转角度α等于（）

A . 36° B . 30° C . 25° D . 22.5°

答案解析收藏纠错 + 选题
9. (2022·定海模拟) 如图，是一块矩形场地 $\text{[math]}$ ，宽 $\text{[math]}$ 米，长 $\text{[math]}$ 米.若在其对角线 $\text{[math]}$ ， $\text{[math]}$ 的延长线上取点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，扩建为新的矩形场地，左、右各增加了0.6米，上、下各增加了 $\text{[math]}$ 米，则 $\text{[math]}$ 的值为（）

A . 0.2 B . 0.3 C . 0.4 D . 0.5

答案解析收藏纠错 + 选题
10. (2022·定海模拟) 如图1，矩形方框内是一副现代智力七巧板，它由两个半圆①和⑦、 $\text{[math]}$ ⑥、等腰直角三角形②和都含 $\text{[math]}$ 角的角不规图形③、直角梯形④、圆不规图形⑤组成，已知 $\text{[math]}$ .如图2，在矩形 $\text{[math]}$ 内，这个智力七巧板恰好能拼成一个滑滑梯，若 $\text{[math]}$ 的直径是2，则矩形 $\text{[math]}$ 的周长为（）

A . 32 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023八上·船营期中) 边长为a、b的长方形，它的周长为14，面积为10，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
12. (2022·定海模拟) 已知关于x，y的二元一次方程组 $\text{[math]}$ 的解是 $\text{[math]}$ 则关于x，y的二元一次方程组 $\text{[math]}$ 的解为

答案解析收藏纠错 + 选题
13. (2022·定海模拟) 已知 $\text{[math]}$ ，那么 $\text{[math]}$ 的值等于.

答案解析收藏纠错 + 选题
14. (2023七下·鸡西期末) 如图是一片枫叶标本，其形状呈“掌状五裂型”，裂片具有少数突出的齿．将其放在平面直角坐标系中，表示叶片“顶部” $\text{[math]}$ ， $\text{[math]}$ 两点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ，则叶杆“底部”点 $\text{[math]}$ 的坐标为．

答案解析收藏纠错 + 选题
15. (2022·定海模拟) 如图，将四边形 $\text{[math]}$ 绕顶点A顺时针旋转 $\text{[math]}$ 至四边形 $\text{[math]}$ 的位置，若 $\text{[math]}$ ，则图中阴影部分的面积为 $\text{[math]}$ .

答案解析收藏纠错 + 选题
16. (2024九上·义乌月考) 准备在一个“7”字型遮阳棚下安装一个喷水装置（如图1），已知遮阳棚DB与竖杆OB垂直，遮阳棚的高度OB＝3米，喷水点A与地面的距离OA＝1米（喷水点A喷出来的水柱呈抛物线型），水柱喷水的最高点恰好是遮阳棚的C处，C到竖杆的水平距离BC＝2米（如图2），此时水柱的函数表达式为，现将遮阳棚BD绕点B向上旋转45°（如图3），则此时水柱与遮阳棚的最小距离为米.（保留根号）

答案解析收藏纠错 + 选题

三、解答题

17. (2022·定海模拟)
1. （1）计算： $\text{[math]}$
2. （2）求代数式的值： $\text{[math]}$ ，其中 $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2022·定海模拟) 如图为某住宅区的两幢10层住宅楼，由地面向上依次为第1层、第2层……第10层，底层和顶层因实际需求层高设计为 $\text{[math]}$ ，其余层高均为 $\text{[math]}$ ，两楼间的距离 $\text{[math]}$ .现需了解甲楼对乙楼采光的影响情况.设太阳光线与水平线的夹角为 $\text{[math]}$ .
1. （1）当 $\text{[math]}$ 是多少度时，甲楼的影子刚好落在乙楼第1层底部？
2. （2）小明家住乙楼的第4层，从（1）中的这一时刻算起，若 $\text{[math]}$ 每小时减少 $\text{[math]}$ ，1小时30分钟后，甲楼的影子对小明家的采光是否有影响？（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
答案解析收藏纠错 + 选题
19. (2022·定海模拟) 图①②都是由边长为1的小等边三角形组成的正六边形，已经有5个小等边三角形涂上阴影，请在余下的空白小等边三角形中，分别按下列要求选取一个涂上阴影.（请将两个小题依次作答在图①，图②中，均只需画出符合条件的一种情形）
1. （1）使得6个阴影小等边三角形组成的图形是轴对称图形，但不是中心对称图形.
2. （2）使得6个阴影小等边三角形组成的图形既是轴对称图形，又是中心对称图形.
答案解析收藏纠错 + 选题
20. (2021八下·衢州期末) 某校举行“衢州有礼八个一”知识问答竞赛.每班选20名同学参加比赛，根据答对的题目数量，得分等级分为5分，4分，3分，2分，学校将八年级甲班和乙班的成绩整理并绘制成如下的统计图.
1. （1）请把甲班知识问答成绩统计图补充完整；
2. （2）通过统计得到如表，请求出表中数据a，b的值.
  班级
  平均数（分）
  中位数（分）
  众数（分）
  甲班
  a
  4
  4
  乙班
  3.6
  3.5
  b
3. （3）根据（2）的结果，你认为甲，乙两班哪个班级成绩更好？写出你的理由.
答案解析收藏纠错 + 选题
21. (2022·定海模拟) 如图，四边形 $\text{[math]}$ 是 $\text{[math]}$ 的内接四边形， $\text{[math]}$ 平分 $\text{[math]}$ ，连结 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 等于 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题

22. (2022·定海模拟) 为了节能减排，某公司从2018年开始投入技术改进资金，经技术改进后产品的成本不断降低，具体数据如表：

年度	2018	2019	2020	2021
投入技术改进资金x万元	2.5	3	4	4.5
产品成本y万元	14.4	12	9	8

（1）分析表中数据，请从一次函数和反比例函数中确定一个函数表示其变化规律，求出y与x的函数关系式，并说明理由；
（2）若2022年公司打算投入技术改进资金5万元，预计2022年产品成本比2021年降低多少万元？
（3）若2023年公司打算把投入技术改进资金x和产品成本y之和控制在12万元，请分别求出投入技术改进资金和产品成本.

答案解析收藏纠错 + 选题

23. (2022·定海模拟) 定义：三角形一边上的点将该边分为两条线段，且这两条线段的积等于这个点到这边所对顶点连线的平方，则称这个点为三角形该边的“好点”.如图1，△ABC中，点D是BC边上一点，连接AD，若AD²＝BD•CD，则称点D是△ABC中BC边上的“好点”.
1. （1）如图2，△ABC的顶点是4×4网格图的格点，请在图中画出AB边上的“好点”；
2. （2）如图3，△ABC是⊙O的内接三角形，点H在AB上，连接CH并延长交⊙O于点D.若点H是△BCD中CD边上的“好点”.
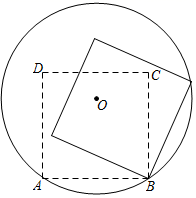
  ①求证：OH⊥AB；
  
  ②若OH∥BD，⊙O的半径为r，且r＝3OH，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
24. (2022·定海模拟) 如图
1. （1）【基础巩固】
  如图1，AC∥DF，Rt△ABC≌Rt△DEF，连结AD，BE，求证：四边形ABED是平行四边形.
2. （2）【尝试应用】
  如图2，在平面直角坐标系xOy中，已知点A，B的坐标分别是A（1，3），B（4，1），点C在x轴上，点D在y轴上.若以AB为边，其余两个顶点为C，D的四边形是平行四边形，求点C，D的坐标.
3. （3）【拓展提高】
  如图3，抛物线y＝x²﹣4x+3与直线y＝x+3交于C，D两点，点E是抛物线上任意一点，在对称轴上是否存在点F，使得以CD为边，其余两个顶点为E，F的四边形是平行四边形，若存在，求出点E的坐标，若不存在，请说明理由.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省舟山市定海区第七中学2022年中考适应性考试数学试卷

副标题：

*注意事项：

浙江省舟山市定海区第七中学2022年中考适应性考试数学试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

班级	平均数（分）	中位数（分）	众数（分）
甲班	a	4	4
乙班	3.6	3.5	b