陕西省渭南市2021年中考数学冲刺试题（a卷）

更新时间：2024-07-13 浏览次数：79 类型：中考模拟

一、单选题

1. (2021七上·遵化期中) 如图，数轴上被墨水遮盖的数可能为（）

A . -1 B . -1.5 C . -3 D . -4.2

答案解析收藏纠错 + 选题
2. (2021·渭南模拟) 下列关于“健康防疫“标志的图中是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·平乐模拟) 下列计算的结果是x⁵的为（）

A . x¹⁰÷x² B . x⁶﹣x C . x²•x³ D . （x²）³

答案解析收藏纠错 + 选题
4. (2021·渭南模拟) 已知正比例函数y＝（2m﹣6）x的图象上一点（x₀ ， y₀），且 $\text{[math]}$ ＜0，则m的取值范围是（）

A . m＞3 B . m＞ $\text{[math]}$ C . m＜ $\text{[math]}$ D . m＜3

答案解析收藏纠错 + 选题
5. (2021·渭南模拟) 如图，Rt△ABC中，∠ACB = 90°，AB = 5，AC= 3，把Rt△ABC沿直线BC向右平移3个单位长度得到△A'B'C' ，则四边形ABC'A'的面积是（）

A . 15 B . 18 C . 20 D . 22

答案解析收藏纠错 + 选题
6. (2021·渭南模拟) 下列图形都是由同样大小的实心圆点按一定规律组成的，其中第①个图形一共有5个实心圆点，第②个图形一共有8个实心圆点，…，按此规律排列下去，第⑨个图形中实心圆点的个数为（）

A . 23 B . 25 C . 27 D . 29

答案解析收藏纠错 + 选题
7. (2021·渭南模拟) 如图四边形ABCD内接于⊙O，弧AB＝弧AD，连接BD，若∠DCE＝50°，则∠ABD的度数为（）

A . 50° B . 60° C . 65° D . 70°

答案解析收藏纠错 + 选题
8. (2021·渭南模拟) 已知二次函数的解析式为 $\text{[math]}$ ， $\text{[math]}$ ，若函数过 $\text{[math]}$ 和 $\text{[math]}$ 两点，则 $\text{[math]}$ 的取值范围（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2023七下·襄城期末) 若一个数的平方等于5，则这个数等于。

答案解析收藏纠错 + 选题
10. (2024九下·杭州模拟) 因式分解： $\text{[math]}$ .

答案解析收藏纠错 + 选题
11. (2021·渭南模拟) 如图，EC，BD是正五边形ABCDE的对角线，则∠1的大小为．

答案解析收藏纠错 + 选题
12. (2021·渭南模拟) 某地2021年3月份接种新冠病毒疫苗的有1万人次，5月份接种新冠病毒疫苗的有1.21万人次，从3月份到5月份，该地接种新冠病毒疫苗人次平均每月的增长率．

答案解析收藏纠错 + 选题
13. (2021·汉滨模拟) 直线y＝2x＋b与反比例函数y＝ $\text{[math]}$ 的图象交于A（1，m），B（﹣2，n）两点，点C（2，t）也在该反比例函数的图象上，则m，n，t的大小关系为．（用“＜“连接）

答案解析收藏纠错 + 选题
14. (2021·渭南模拟) 如图，已知正方形ABCD中，AB＝6，点E是边AD的中点，点P是边CD上的动点，点Q是正方形内一动点，且满足∠BQC＝90°，则PE＋PQ的最小值是．

答案解析收藏纠错 + 选题

三、解答题

15. (2021·渭南模拟) 计算：（ $\text{[math]}$ ）× $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2021·渭南模拟) 解不等式组： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
17. (2021·渭南模拟) 先化简 $\text{[math]}$ ，然后从 $\text{[math]}$ ，0，1，3中选一个合适的数代入求值．

答案解析收藏纠错 + 选题
18. (2021·渭南模拟) 如图，点P为∠AOB内一定点，过点P作PD⊥OA于点D，请用尺规作图法在OB上求作一点Q，使得∠AOB与∠DPQ互补（保留作图痕迹，不写作法）．

答案解析收藏纠错 + 选题
19. (2021·渭南模拟) 如图，在▱ABCD中，E、F为对角线AC上两点，且BE∥DF，请从图中找出一对全等三角形，并证明．

答案解析收藏纠错 + 选题
20. (2021·渭南模拟) 为庆祝中国共产党成立100周年，在校园内传承红色文化，弘扬爱国主义奋斗精神，某校每月都要开展以“从小学党史永远跟党走”为主题的知识测评活动．为了激发学生的积极性，该校对达到一定成绩的学生授予“小小楷模“的荣誉称号，为了确定一个适当的奖励目标，该校随机选取了七年级20名学生在5月份测评的成绩，数据如下：
收集数据：90 91 89 89 90 98 90 97 95 98 98 97 95 88 90 97 95 90 95 88
1. （1）根据上述数据将下列表格补充完整．
  整理、描述数据：
  成绩/分
  88
  89
  90
  91
  95
  97
  98
  学生人数
  2
  2
  1
  4
  3
  数据分析：样本数据的平均数、众数和中位数如下表（单位：分）
  平均数
  众数
  中位数
  90
2. （2）数据应用：根据数据分析，该校决定在七年级授予测评成绩前30%的学生“小小楷模”荣誉称号，请估计评选该荣誉称号的最低分数并说明理由．
答案解析收藏纠错 + 选题

21. (2021·渭南模拟) 宝鸡市文化景观标志“天下第一灯”（如图），为中国最高的开启式景观灯，曾获大世界基尼斯之最．某综合与实践小组开展了测量“天下第一灯”高度的实践活动．他们分成三组制订了不同测量方案，并利用课余时间完成了实地测量，测量数据如表：

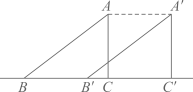
课题	测量“天下第一灯”（AB）的高度
测量工具	测量角度的仅器，标杆，皮尺等
测量小组	第一组	第二组	第三组
测量方案示意图
说明	EF是标杆，甲同学站在H处观察到标杆顶端E和点A恰好在一条直线上，点H、F、B在一条直线上	CH是“天下第一灯”（AB）旁的一个临时点C、D、B在一条直线上	点C、D、B在同一条直线上
测量数据	甲同学的身高PH＝1.5米，EF＝3米，HF＝2米，BF＝40米	从点G处测得A点的仰角为37°，测得B点的俯角为45°	从点C处测得A点的仰角为37°，从点D处测得A点的仰角为45°，CD＝11米

（1）根据测量方案和所得数据，第小组的数据无法算出天下第一灯”的高度AB；
（2）请选择其中一个可行方案及其测量数据，求出“天下第一灯”的高度AB．（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75）

答案解析收藏纠错 + 选题

22. (2021·渭南模拟) 如图①是第十四届全运会会徽“礼天玉璧”，其主色调黄、绿、蓝、紫、红分别象征黄土高原、自然生态、现代科技、时尚文化、革命圣地，呈现中华民族伟大复兴的深厚历史渊源和广泛现实基础某校组织开展宣讲活动，每位同学可从这五种色调所象征的意义中选择一个作为宣讲主题，小军和小华准备通过摸球游戏确定自己的宣讲主题游戏规则．
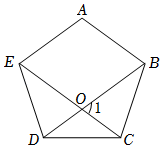
如图②，在一个不透明的袋中装有黄、绿、蓝、紫、红五个小球（小球除颜色外无任何区别），小军和小华先后从袋中随机摸出一球（不放回）并把摸出小球的颜色所对应的象征意义作为各自的宣讲主题．
1. （1） “小军从袋中摸出红球”这一事件是事件；（填“必然”、“不可能”或“随机”）
2. （2）利用树状图或列表法求小军和小华中有一人的宣讲主题是“革命圣地”的概率．
答案解析收藏纠错 + 选题
23. (2021·渭南模拟) 小王计划从某批发市场批量购买A、B两种仿古秦兵马俑工艺品摆件，已知A种摆件的批发价比B种摆件的批发价每个少5元，且用400元购买的A种摆件数量与用500元购买的B种摆件数量相同．
1. （1）求A、B两种摆件的单价各是多少？
2. （2）凭会员卡在此批发市场购买商品可以获得8折优惠，会员卡费用为50元，若小王购买会员卡并用此卡按需购买100个仿古秦兵马俑工艺品摆件，共用了y元，设A种摆件购买了x个，请求出y与x之间的函数关系式．若小王共用了1930元，则他购买A、B两种摆件各多少个？
答案解析收藏纠错 + 选题
24. (2021·渭南模拟) 如图，在△ABC中，∠ACB＝90°，边AB与⊙O相切于点D，CD是⊙O的直径，AC交⊙O于E，连接BE交CD于P，交⊙O于F，连接DF．
1. （1）求证：∠ABC＝∠EFD；
2. （2）若AD＝2，CD＝ $\text{[math]}$ ，求BD的长．
答案解析收藏纠错 + 选题
25. (2021·渭南模拟) 如图，在平面直角坐标系中抛物线L：y＝﹣x²＋bx＋c的图象与x轴的一个交点为A（﹣3，0），顶点B的横坐标为﹣1
1. （1）求抛物线L的函数表达式；
2. （2）点P为坐标轴上一点将抛物线L绕点P旋转180后得到抛物线L′，且A、B的对应点分别为C、D，当以A、B、C、D为顶点的四边形是矩形时，请求出符合条件的点P坐标．
答案解析收藏纠错 + 选题
26. (2021·渭南模拟) 如图
1. （1）如图①，在△ABC中，AB＝AC＝2，∠A＝120°，则S_△ABC＝；
2. （2）如图②，在△ABC中，AB的垂直平分线交BC于D，交AB于点M，AC的垂直平分线交BC于E，交AC于N，∠DAE＝20°，BC＝6，求∠BAC的度数及△ADE的周长；
3. （3）如图③，某农场主欲规划出一个如图所示的矩形田地ABCD，其中BC＝0.4km，点P在边AD上，E、F为BC边上两点（包括端点），在△PEF区域种植甲种农作物，其余区域种植乙种农作物，并沿△PEF的三边铺设围栏，围栏总长为0.6km（即△PEF的周长为0.6km），围栏PE与PF的夹角为60°（即∠EPF＝60°），为了尽可能多的种植农作物要求矩形ABCD的面积尽可能的大，请问能否设计出一个面积尽可能大又满足要求的矩形ABCD田地？若能，求出矩形ABCD面积的最大值；若不能，请说明理由．
答案解析收藏纠错 + 选题