河南省信阳市固始县2022年九年级下学期第一次适应性考试数学...

更新时间：2024-07-13 浏览次数：91 类型：中考模拟

一、单选题

1. (2023七下·永安期中) 下列有理数中最大的数是（）

A . 0 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022·固始模拟) 2022年1月20日，河南省统计局公布2021年全省地区生产总值为58887.41亿元，同比增长6.3%.这里的近似数“58887.41亿”是精确到（）

A . 百万位 B . 亿位 C . 万位 D . 百分位

答案解析收藏纠错 + 选题
3. (2022·大理模拟) 下列用相同的正方体堆放在一起组成的几何体中，主视图和左视图不相同的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022·固始模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022·固始模拟) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2022·濠江模拟) 已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 都在反比例函数 $\text{[math]}$ 的图象上，那么 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·固始模拟) 西峡猕猴桃，河南省西峡县特产，中国国家地理标志产品.种植户小王新摘了一批猕猴桃，这些猕猴桃的质量的平均数和方差分别是 $\text{[math]}$ ， $\text{[math]}$ ，小王从中选出质量大且均匀的猕猴桃作为一等品销售，一等品猕猴桃的质量的平均数和方差分别为 $\text{[math]}$ ， $\text{[math]}$ ，则下列结论一定成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·固始模拟) 对于实数m，n，定义一种运算“ $\text{[math]}$ ”为 $\text{[math]}$ ，例如， $\text{[math]}$ 那么不等式组 $\text{[math]}$ 的解集在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2022·固始模拟) 如图，边长为2的正六边形 $\text{[math]}$ 放置于平面直角坐标系中，边 $\text{[math]}$ 在x轴的负半轴上，顶点B在y轴正半轴上，将正六边形 $\text{[math]}$ 绕坐标原点O旋转 $\text{[math]}$ 后，顶点D恰好落在双曲线上，那么该双曲线是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·固始模拟) 如图，已知 $\text{[math]}$ ， $\text{[math]}$ ，按以下步骤作图：①以点A为圆心，以适当长为半径画弧，分别交边 $\text{[math]}$ ， $\text{[math]}$ 于点M，N；②分别以M，N为圆心，以大于 $\text{[math]}$ 的长为半径画弧，两弧在 $\text{[math]}$ 的内部相交于点P；③作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点D；④分别以A，D为圆心，以大于 $\text{[math]}$ 的长为半径画弧，两弧相交于点G，H；⑤作直线 $\text{[math]}$ ，分别交 $\text{[math]}$ ， $\text{[math]}$ 于点E，F，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·秦都期中) 若 $\text{[math]}$ ，则 $\text{[math]}$ =.

答案解析收藏纠错 + 选题
12. (2022·固始模拟) 若关于x的分式方程 $\text{[math]}$ 的解为正数，则m的取值范围是.

答案解析收藏纠错 + 选题
13. (2022·固始模拟) 2022年冬奥会吉祥物为“冰墩墩”，冬残奥会吉祥物为“雪容融”.如图，现有三张正面印有吉祥物的不透明卡片，卡片除正面图案不同外，其余均相同，其中两张正面印有冰墩墩图案，一张正面印有雪容融图案，将三张卡片正面向下洗匀，从中随机抽取一张卡片，记下图案后正面向下放回，洗匀后再从中随机抽取一张卡片，则抽出的两张卡片图案都是冰墩墩的概率是.

答案解析收藏纠错 + 选题
14. (2022·固始模拟) 如图，已知 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则经过A，B，C三点的 $\text{[math]}$ 的长度为.

答案解析收藏纠错 + 选题
15. (2022·固始模拟) “希望小组”的同学们利用课余时间对“纸片中的折叠问题”进行了探究.如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点D是 $\text{[math]}$ 边上不与端点B，C重合的一个动点，第一步，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点B的对应点为 $\text{[math]}$ ；第二步，将 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，点D的对应点为 $\text{[math]}$ ，当直线 $\text{[math]}$ 过 $\text{[math]}$ 的一个顶点时，线段 $\text{[math]}$ 的长度为.

答案解析收藏纠错 + 选题

三、解答题

16. (2022·固始模拟) 化简与计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2022·固始模拟) 为落实教育部“双减”政策，某市从2021年9月起，各中小学全面开展课后延时服务.为了了解该市甲、乙两所中学延时服务的情况，在这两所学校分别随机抽查了100名家长进行问卷调查.家长对延时服务的综合评分记为x，将所得数据分为5个等级（A“很满意”： $\text{[math]}$ ；B“满意”： $\text{[math]}$ ； $\text{[math]}$ “比较满意”： $\text{[math]}$ ；D“不太满意”： $\text{[math]}$ ；E“不满意”： $\text{[math]}$ ），将数据进行整理后，得到如下统计图和统计表.
①甲中学延时服务得分的扇形统计图
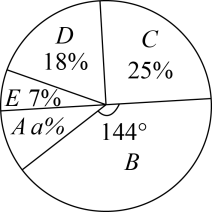
②乙中学延时服务得分频数分布统计表
等级
满意度
得分
频数
A
很满意
$\text{[math]}$
15
B
满意
$\text{[math]}$
C
比较满意
$\text{[math]}$
30
D
不太满意
$\text{[math]}$
10
E
不满意
$\text{[math]}$
5
③甲、乙两中学延时服务得分的平均数、中位数、众数如下表：
学校
平均数
中位数
众数
甲
78
79.5
80
乙
80
$\text{[math]}$
85
④乙中学的等级“B”的分数从高到低排列，排在最后的10个数据分别是：84，84，83，83，83，81，80，80，80，80.
请你根据以上信息，回答下列问题：
1. （1）直接写出a和b的值；
2. （2）课后延时服务综合得分在70分及以上为合格，请你估计甲中学3000名家长中认为该校课后延时服务合格的人数；
3. （3）小明说：“乙中学的课后延时服务比甲中学好”，你同意小明的说法吗？请写出一条理由.
答案解析收藏纠错 + 选题
18. (2022·固始模拟) 如图，点C是以 $\text{[math]}$ 为直径的半圆O上一动点，作半径 $\text{[math]}$ 的垂直平分线交 $\text{[math]}$ 于点F，交 $\text{[math]}$ 于点E，交切线 $\text{[math]}$ 于点D.
1. （1）判断 $\text{[math]}$ 的形状，并说明理由；
2. （2）若 $\text{[math]}$ 的半径是2， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
19. (2022·固始模拟) 如图，某校大礼堂前墙 $\text{[math]}$ 上悬挂宣传标语 $\text{[math]}$ .为了测量标语 $\text{[math]}$ 的高度，小冬站在大礼堂正前方与点B相距8米的点C处，测得标语上端点A的仰角为 $\text{[math]}$ ，前进2米正好走到台阶M处，台阶高0.2米，在台阶的边沿点E处测得标语下端点D的仰角为 $\text{[math]}$ ，求标语 $\text{[math]}$ 的高度.（结果精确到0.01米，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
20. (2022·固始模拟) 在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线 $\text{[math]}$ 上，其中 $\text{[math]}$
1. （1）求抛物线的对称轴；
2. （2）若 $\text{[math]}$ ，比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系，并说明理由.
答案解析收藏纠错 + 选题
21. (2022·固始模拟) 喜万家超市以原价为20元/瓶的价格对外销售某种洗手液，为了减少库存，决定降价销售，经过两次降价后，售价为16.2元/瓶.
1. （1）求平均每次降价的百分率；
2. （2）为确保新学期开学工作安全、卫生、健康、有序，某学校决定购买一批洗手液（超过200瓶）.超市对购买量大的客户有优惠措施，在16.2元/瓶的基础上推出方案一：每瓶打九折；方案二：不超过200瓶的部分不打折，超过200瓶的部分打八折，学校应该选择哪种方案更省钱（只能选择一种）？请说明理由.
答案解析收藏纠错 + 选题

22. (2022·固始模拟) 九（1）班数学兴趣小组的同学参照学习函数的过程与方法，探究函数 $\text{[math]}$ 的图象与性质，他们的探究过程如下，请你补充完整.

（1）列表：

x	…	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	0	1	2	3	4	5	6	7	…
y	…	m	0	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	0	5	n	$\text{[math]}$	$\text{[math]}$	1	…

表中m=，n=.

（2）描点、连线：
如图，在平面直角坐标系中，根据上表中数据以自变量x的值为横坐标，以相应的函数值y为纵坐标，描出了部分对应点，请你描出剩余的点，并画出该函数的图象.
（3）探究性质，解决问题：
①试写出该函数的一条性质：；

②当 $\text{[math]}$ 时，函数 $\text{[math]}$ 的自变量x的取值范围是；

③若直线 $\text{[math]}$ 与函数 $\text{[math]}$ 的图象有三个不同的交点，请直接写出k的取值范围.

答案解析收藏纠错 + 选题

23. (2022·固始模拟) 数学综合与实践课上，同学们以“三角形的旋转”为主题开展探究活动，如图，小东同学把等腰直角三角板 $\text{[math]}$ 的直角顶点C绕着直角三角板 $\text{[math]}$ 的斜边中点旋转，其中 $\text{[math]}$ ，直线 $\text{[math]}$ ， $\text{[math]}$ 相交于点G，边 $\text{[math]}$ 与 $\text{[math]}$ 相交于点H.
1. （1）如图①，当 $\text{[math]}$ 时，线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是；
2. （2）将图①中的 $\text{[math]}$ 旋转到如图②所示的位置，请判断线段 $\text{[math]}$ 与 $\text{[math]}$ 的数量关系是否发生变化，并说明理由.
3. （3）在（2）的情况下，若 $\text{[math]}$ 绕点C旋转时，边 $\text{[math]}$ 与 $\text{[math]}$ 的交点H始终在线段 $\text{[math]}$ 上，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，请直接写出线段 $\text{[math]}$ 的长度.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

河南省信阳市固始县2022年九年级下学期第一次适应性考试数学...

副标题：

*注意事项：

河南省信阳市固始县2022年九年级下学期第一次适应性考试数学...

试题分析

总体分析

题量分析

难度分析

知识点分析

等级	满意度	得分	频数
A	很满意	$\text{[math]}$	15
B	满意	$\text{[math]}$
C	比较满意	$\text{[math]}$	30
D	不太满意	$\text{[math]}$	10
E	不满意	$\text{[math]}$	5

学校	平均数	中位数	众数
甲	78	79.5	80
乙	80	$\text{[math]}$	85