湖南省长沙市青竹湖湘一外国语学校2021-2022学年九年级...

更新时间：2024-07-31 浏览次数：126 类型：月考试卷

一、单选题

1. (2022七上·新昌月考) -2022的绝对值是（）

A . 2022 B . -2022 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022九下·长沙月考) 2021年2月10日19时52分，中国首次火星探测任务“天问一号”探测器成功“刹车”被火星“捕获”.在制动捕获过程中，探测器距离地球的距离为192000000公里，数字192000000用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023七下·新邵期末) 第24届冬季奥林匹克运动会将于2022年2月4日至2月20日在中国北京市和张家口市联合举办．以下是历届的冬奥会会徽设计的部分图形，其中不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022九下·长沙月考) 下列计算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022七下·承德期末) 如图，已知AB∥CD，AF交CD于点E，且BE⊥AF，∠BED＝50°，则∠A的度数是（　　）

A . 40° B . 50° C . 80° D . 90°

答案解析收藏纠错 + 选题
6. (2023八下·乌鲁木齐期末) 下列命题为真命题的是（）

A . 同旁内角互补 B . 三角形的外心是三条内角平分线的交点 C . 平行于同一条直线的两条直线平行 D . 若甲、乙两组数据中， $\text{[math]}$ ， $\text{[math]}$ ，则乙组数据较稳定

答案解析收藏纠错 + 选题
7. (2022九下·长沙月考) 如图：△AOB与△A₁OB₁是以原点为位似中心的位似图形，且位似比为1：3，点B的坐标为（﹣1，2），则点B₁的坐标为（　　）

A . （2，﹣4） B . （﹣2，4） C . （3，﹣6） D . （3，6）

答案解析收藏纠错 + 选题
8. (2024七上·沂源期末) 对于函数y=-3x+1，下列结论正确的是（）

A . 它的图象必经过点(1，3) B . y的值随x值的增大而增大 C . 当x＞0时，y＜0 D . 它的图象与x轴的交点坐标为( $\text{[math]}$ ， 0)

答案解析收藏纠错 + 选题
9. (2022七下·高邑期中) 如图，将Rt△ABC沿着点B到点C的方向平移到△DEF的位置，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则图中阴影部分的面积为（）

A . 12 B . 15 C . 18 D . 24

答案解析收藏纠错 + 选题
10. (2022九下·长沙月考) 一只小虫子欲从A点不重复经过图中的点或者线段，而最终到达目的地E，这只小虫子的不同走法共有（）

A . 12种 B . 13种 C . 14种 D . 15种

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·西安期末) 分解因式： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2022九下·长沙月考) 如图，AB为⊙O的弦，半径OC⊥AB，垂足为D，如果AB＝8cm，CD＝2cm，那么⊙O的半径是cm.

答案解析收藏纠错 + 选题
13. (2022九下·长沙月考) 已知扇形的圆心角为120°，弧长为12πcm，则扇形的半径为cm.

答案解析收藏纠错 + 选题
14. (2022九下·长沙月考) 若分式方程 $\text{[math]}$ ＋ $\text{[math]}$ ＝3无解，则m的值是.

答案解析收藏纠错 + 选题
15. (2022九下·长沙月考) 如图，AD、AF分别是△ABC的高和角平分线，已知∠B＝36°，∠C＝76°则∠DAF＝度.

答案解析收藏纠错 + 选题
16. (2022九下·长沙月考) 如图，直线 $\text{[math]}$ （ $\text{[math]}$ ）与双曲线 $\text{[math]}$ 相交于A，B两点，点C在第三象限，且 $\text{[math]}$ //x轴， $\text{[math]}$ //y轴，则△ABC面积的最小值为.

答案解析收藏纠错 + 选题

三、解答题

17. (2022九下·长沙月考) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
18. (2022九下·长沙月考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ .

答案解析收藏纠错 + 选题
19. (2022九下·长沙月考) 如图，在平行四边形ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于 $\text{[math]}$ BF的相同长为半径画弧，两弧交于点P，连接AP并延长交BC于点E，连接EF.
1. （1）根据以上尺规作图的过程，证明四边形ABEF是菱形；
2. （2）若菱形ABEF的边长为6， $\text{[math]}$ ，求菱形ABEF的面积.
答案解析收藏纠错 + 选题

20. (2022九下·长沙月考) 为了了解我市中学生参加“科普知识”竞赛成绩的情况，随机抽查了部分参赛学生的成绩，整理并制作出如下的统计表和统计图，如图所示.请根据图表信息解答下列问题：

组别	分数段（分）	频数	频率
A组	60≤x＜70	30	0.1
B组	70≤x＜80	90	n
C组	80≤x＜90	m	0.4
D组	90≤x＜100	60	0.2

（1）在表中：m＝，n＝；
（2）补全频数分布直方图；
（3）小明的成绩是所有被抽查学生成绩的中位数，据此推断他的成绩在组；
（4） 4个小组每组推荐1人，然后从4人中随机抽取2人参加颁奖典礼，恰好抽中A、C两组学生的概率是多少？并列表或画树状图说明.

答案解析收藏纠错 + 选题

21. (2022九下·长沙月考) 已知关于x的一元二次方程 $\text{[math]}$ ，其中a，b，c分别为△ABC三边的长.
1. （1）如果x=2是方程的根，则△ABC的形状为；
2. （2）如果方程有两个相等的实数根，试判断△ABC的形状，并说明理由；
3. （3）如果△ABC是等边三角形，试求这个一元二次方程的根.
答案解析收藏纠错 + 选题
22. (2022九下·长沙月考) 某物流公司租用A、B两种型号的车运送货物：用2辆A型车和1辆B型车装满货物一次可运货10吨；用1辆A型车和2辆B型车装满货物一次可运货11吨.公司现有31吨货物，计划同时租用两种型号的车，一次运完，且恰好每辆车都装满货物.
1. （1） 1辆A型车和1辆B型车都装满货物一次可分别运货多少吨？
2. （2）如果租用A型车a辆，B型车b辆，请你帮该物流公司设计租车方案；
3. （3）若A型车每辆需租金100元/次，B型车每辆需租金120元/次.请选出最省钱的租车方案，并求出最少租车费.
答案解析收藏纠错 + 选题
23. (2022九下·长沙月考) 已知关于x的函数 $\text{[math]}$ （k为常数，且 $\text{[math]}$ ）与函数 $\text{[math]}$ ，定义 $\text{[math]}$ 与 $\text{[math]}$ 的“和函数”为 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的“和函数”的解析式为；
2. （2）若 $\text{[math]}$ 与 $\text{[math]}$ 的“和函数”为 $\text{[math]}$ ，求k，b的值；
3. （3）若 $\text{[math]}$ 与 $\text{[math]}$ 的“和函数”的顶点为P（m，n），求n关于m的关系式.
答案解析收藏纠错 + 选题
24. (2022九下·长沙月考) 如果一个三角形能被一条线段分割成两个等腰三角形，则称这个三角形为“至善三角形”.称这条线段为该三角形的“润心线段”.
1. （1）下列三角形一定是“至善三角形”的是____；
  
  A . 等边三角形 B . 直角三角形 C . 等腰三角形
2. （2）下列说法正确的有（填序号）
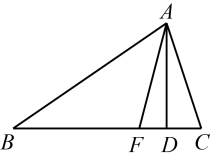
  ①若一个三角形的两个内角分别是36°、72°，则这个三角形是“至善三角形”
  
  ②若一个三角形的两个内角分别是27°、81°，则这个三角形是“至善三角形”
  
  ③若一个三角形的一个内角是另一个内角的2倍，则这个三角形一定是“至善三角形”
  
  ④若一个三角形的一个内角是另一个内角的3倍，则这个三角形一定是“至善三角形”
3. （3）如图，直线l与x轴、y轴的正半轴分别交于A、B两点，点B的坐标为（0，2），且 $\text{[math]}$ ，若△ABO为“至善三角形”，且抛物线 $\text{[math]}$ 经过其“润心线段”的两个端点，求此抛物线的解析式.
答案解析收藏纠错 + 选题
25. (2022九下·长沙月考) 如图，四边形ABCD为⊙O的圆内接四边形，AC=AD，点B为 $\text{[math]}$ 的中点，点E为AC上一点，且 $\text{[math]}$ ， F为直径AG的延长线上一点，且∠FDG=∠FAD.
1. （1）求证：DF是⊙O的切线；
2. （2）若∠BCA=55°，∠BAC=15°，求∠F的度数；
3. （3）若AC=AD=a，求 $\text{[math]}$ 的最大值（用含a的式子表示）.
答案解析收藏纠错 + 选题