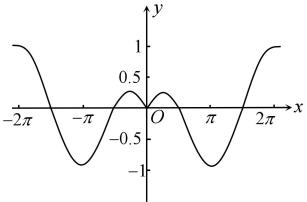
4.
(2022·贵阳模拟)
2021年11月24日,贵阳市修文县发生了4.6级地震,所幸的是没有人员伤亡和较大财产损失,在抗震分析中,某结构工程师提出:由于实测地震记录的缺乏,且考虑到强震记录数量的有限性和地震动的不可重复性,在抗震分析中还需要人工合成符合某些指定统计特征的非平稳地震波时程,其中地震动时程强度包络函数

,

(单位:秒)分别为控制强震平稳段的首末时刻;

(单位:秒)表示地震动总持时;

是衰减因子,控制下降段衰减的快慢.在一次抗震分析中,地震动总持时是20秒,控制强震平稳段的首末时刻分别是5秒和10秒,衰减因子是0.2,则当

秒时,地震动时程强度包络函数值是( )
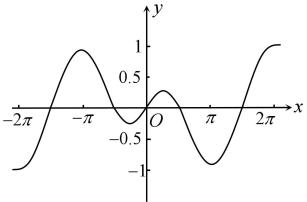 B .
B .  C .
C . 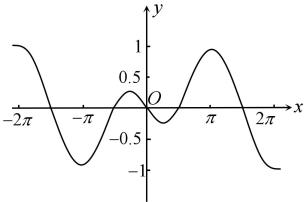 D .
D .