山西省临汾侯马市2022年九年级学业水平考试模拟测评（二）数...

更新时间：2022-09-27 浏览次数：149 类型：期末考试

一、单选题

1. 下列有理数比较大小，结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 下列运算结果正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 数学课上，老师在组织同学们探索多边形的内角和公式时，同学们提出了将此问题转化为已学的三角形内角和知识进行探索的思路．如图是四名同学探索多边形内角和公式时运用的不同的分割方法，将多边形转化为多个三角形，并得出了相同的结论．这四名同学在探索过程中主要体现的数学思想是（）

A . 建模思想 B . 分类讨论思想 C . 数形结合思想 D . 转化思想

答案解析收藏纠错 + 选题
4. 盾构机是用于铁路、公路、地铁和水利等基建工程的隧道工程机械.2008年我国研发制造了第一台复合式土压平衡盾构机——中国中铁1号．如图是我国迄今为止研制的最大直径的盾构机，开挖直径达16.07m ，整机长150m ，总重量4300t ．数据“4300t”转化成千克用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 如图，将一副三角尺按如图所示的位置在同一平面内摆放，其中∠ACB＝∠CED＝90°，∠B＝30°，∠ECD＝45°．若 $\text{[math]}$ ，CB与DE相交于点F ，则∠BCD的度数为（）

A . 15° B . 20° C . 25° D . 30°

答案解析收藏纠错 + 选题

6. 某校准备选派甲、乙、丙、丁中的一名队员代表学校参加全市跳绳比赛，下表是这四名队员选拔赛成绩的平均数和方差，你觉得最适合的队员是（）

	甲	乙	丙	丁
平均数/（个/分）	201	180	201	180
方差	13	5.5	2.4	2.4

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题

7. 不等式组 $\text{[math]}$ 的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. 如图是某公园在一长35m，宽23m的矩形湖面上修建的等宽的人行观景曲桥，它的面积恰好为原矩形湖面面积的 $\text{[math]}$ ，求人行观景曲桥的宽．若设人行观景曲桥的宽为xm，则x满足的方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. 将如图所示的无盖正方体沿边AB ， BC ， DE ， EF剪开后展开，则下列展开图的示意图正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
10. 山西著名工艺品平遥推光漆器外观古朴雅致、闪光发亮，绘饰金碧辉煌，以手掌推出光泽而得名．图1是平遥推光漆器的一种图案，图2是选取其某部分并且放大后的示意图．四边形ABCD是边长为2的正方形，分别以正方形的四个顶点为圆心， $\text{[math]}$ 对角线的长为半径画弧，四条弧相交于点O ，则图中阴影部分的面积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. 化简 $\text{[math]}$ 的结果是

答案解析收藏纠错 + 选题
12. 如图，AB是半圆O的直径，点C ， D在半圆O上．若∠BDC＝140°，则∠ABC的度数为°．

答案解析收藏纠错 + 选题
13. 如图是一组有规律的图案，它们都是由大小相同的组成的，第1个图案中有5个，第2个图案中有8个，第3个图案中有11个 ……按此规律，第n个图案中有个．（用含n的代数式表示）

答案解析收藏纠错 + 选题
14. 如图，在平面直角坐标系中，以原点O为位似中心，在y轴的同侧作等边三角形 $\text{[math]}$ ，使它与△ABC位似，且相似比为3：1．若四边形 $\text{[math]}$ 是边长为6的菱形，则点A的坐标为．

答案解析收藏纠错 + 选题
15. 如图，四边形ABCD是边长为2的正方形，E为AD边的中点．将△ABE沿BE折叠得到 $\text{[math]}$ ，连接AC ，分别交BE ， $\text{[math]}$ 于点F ， G ，则FG的长为．

答案解析收藏纠错 + 选题

三、解答题

16.
1. （1）计算： $\text{[math]}$ ；
2. （2）下面是小明同学对多项式 $\text{[math]}$ 进行分解因式的过程，请仔细阅读并完成相应的任务．
  
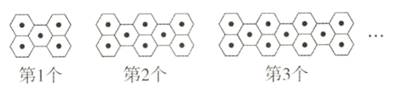
  任务：
  
  ①在上述过程中，第一步所依据的数学公式用字母表示为；
  
  ②第四步分解因式的方法是提公因式法，其依据的运算律为；
  
  ③第步出现错误，错误的原因是；
  
  ④分解因式正确的结果为．
答案解析收藏纠错 + 选题
17. 2022年春节来临之际，各大商场都进行了促销活动．某商场将某品牌的电视机按进价提高60%作为标价，然后以“九折酬宾，再返现金200元”的优惠进行促销，结果该品牌电视机每台仍可获利460元．求该品牌电视机每台的进价．

答案解析收藏纠错 + 选题
18. 如图，正比例函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ ，B为正比例函数图象上一点，过点B作BD⊥y轴于点D ，与反比例函数的图象交于点C ．
1. （1）求反比例函数的表达式及a的值．
2. （2）连接AC ．若BD＝9，求△ABC的面积．
答案解析收藏纠错 + 选题

19. 为落实中央关于“双碳”的战略部署，必须加快推进绿色能源开发利用．绿色电能的主要来源为风能，太阳能等，在生产电力的过程中，绿色电能的二氧化碳排放量为零或趋近于零．为了解风力发电机组每天的发电量（记为Q），现对风力发电机组中每台风力发电机一天的发电量进行了随机调查，并将发电量的数据统计整理成如下不完整的频数分布表和频数直方图：

每台风力发电机一天发电量的频数分布表

发电量Q/万千瓦时	频数	频率
$\text{[math]}$	1	0.025
$\text{[math]}$	2	a
$\text{[math]}$	12	0.3
$\text{[math]}$	b
$\text{[math]}$	9	0.025

每台风力发电机一天发电量的频数直方图

请根据图表中提供的信息，解答下列问题：

（1）直接写出a与b的值．
（2）将频数直方图补充完整．若该风力发电机组共有200台风力发电机，请估计该风力发电机组中一天发电量不少于2.5万千瓦时的风力发电机有多少台？
（3）绿色能源是指不排放污染物，能够直接用于生产生活的能源．某数学兴趣小组为了进一步学习绿色能源的相关知识，收集到如下相应的图片，将其制成卡片（除内容外，其余完全相同）．他们将这四张卡片背面朝上，洗匀放好，从中随机抽取一张，不放回，再从中随机抽取一张，请用列表或画树状图的方法，求抽到的两张卡片恰好是“太阳能热水”和“氢能源汽车”的概率．

答案解析收藏纠错 + 选题

20. 如图1是2022年北京冬奥会首钢滑雪大跳台，曲线的设计灵感来自敦煌“飞天”飘带，又名“雪飞天”，它是世界上首例永久性保留和使用的滑雪大跳台场馆．如图2，为测量“雪飞天”的高度，测得大跳台跨度AB为140m，出发区CD为20m，且 $\text{[math]}$ ，AD为大跳台钢支架，在点A处测得点D的仰角∠DAB＝75°，在点C处测得点B的俯角∠ECB＝30°．（测角仪的高度忽略不计）
1. （1）求大跳台出发区CD距离地面AB的高度．（结果精确到1m；参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）
2. （2）据了解，“雪飞天”需要造雪 $\text{[math]}$ ，分别用雪枪和雪炮来满足对于雪量和雪质的不同要求，雪炮出雪量大，适合室外滑雪场快速铺雪，雪枪造雪分布比较平均，相对造雪量比较小．若每台雪枪每小时出雪量比雪炮少 $\text{[math]}$ ，且一台雪枪出雪 $\text{[math]}$ 所用的时间与一台雪炮出雪 $\text{[math]}$ 所用的时间相等．求每台雪枪和雪炮每小时的出雪量．
答案解析收藏纠错 + 选题
21. 阅读以下材料，并按要求完成相应的任务关于圆的任务．

任务：
1. （1）尺规作图：请根据材料，在图中补全图形．（保留作图痕迹，标明字母，不写作法）．
2. （2）善思小组的同学尝试证明该引理，请按照下面的证明思路，写出该证明的剩余部分．
  证明：连接PA ， PD ， PQ ， QD ．
  
  …
答案解析收藏纠错 + 选题
22.
1. （1）综合与实践
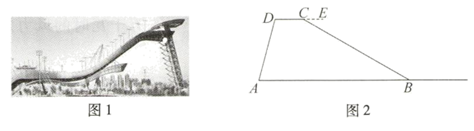
  问题背景：
  
  如图1，在四边形ABCD中，AB＝5，BC＝4，AD⊥CD ，连接AC ， AC⊥BC ，过点C作CE⊥AB于点E ，且CE＝CD ．
  
  求证：AD＝AE ．
2. （2）操作探究：
  如图2，将△ACD沿直线AB方向向右平移一定距离，点A ， C ， D的对应点分别为点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且点 $\text{[math]}$ 与点E重合．
  
  ①连接 $\text{[math]}$ ，试判断四边形 $\text{[math]}$ 的形状，并说明理由；
  
  ②求出△ACD平移的距离．
3. （3）若将△ACD继续沿直线AB方向向右平移，当点 $\text{[math]}$ 恰好落在BC边上时，请在图1中画出平移后的图形，并求出继续平移的距离。
4. （4）拓展创新：
  如图3，在（2）的条件下，将 $\text{[math]}$ 绕点E按顺时针方向旋转一定角度，在旋转的过程中，记直线 $\text{[math]}$ 分别与边AB ， BC交于点N ， M ．
  
  当 $\text{[math]}$ 时，请直接写出BN的长．
答案解析收藏纠错 + 选题
23. 如图，抛物线 $\text{[math]}$ 经过 $\text{[math]}$ ， $\text{[math]}$ 两点，与y轴交于点C ， P为第四象限内抛物线上一点，过点P作PM⊥x轴于点M ，连接AC ， AP ， AP与y轴交于点D ．
1. （1）求抛物线的函数表达式．
2. （2）当∠MPA＝2∠PAC时，求直线AP的函数表达式．
3. （3）在（2）的条件下，在抛物线的对称轴上是否存在点E ，使以E ， M ， C为顶点的三角形是直角三角形？若存在，请直接写出点E的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题