陕西省2022年中考一模数学试卷

更新时间：2022-06-01 浏览次数：129 类型：中考模拟

一、单选题

1. (2022·陕西模拟) 计算 $\text{[math]}$ 的结果是（）

A . 8 B . －8 C . 2 D . －2

答案解析收藏纠错 + 选题
2. 将如图的七巧板的其中几块，拼成一个多边形，为中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022·临沂模拟) 如图，在△ABC中，∠A＝46°，∠B＝72°.若直线l∥BC，则∠1的度数为（　　）

A . 117° B . 120° C . 118° D . 128°

答案解析收藏纠错 + 选题
4. (2022·陕西模拟) 如图，A、B、C是小正方形的顶点，且每个小正方形的边长为1，则sinB的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024九下·辽宁模拟) 在平面直角坐标系中，若将一次函数 $\text{[math]}$ 的图象向左平移3个单位后，得到一个正比例函数的图象，则m的值为（）

A . -5 B . 5 C . -6 D . 6

答案解析收藏纠错 + 选题
6. (2022·陕西模拟) 如图，在矩形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，过矩形的对称中心O的直线EF，分别与AD、BC交于点E、F，且 $\text{[math]}$ 若H为OE的中点，连接BH并延长，与AD交于点G，则BG的长为（）

A . 8 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2022·陕西模拟) 如图，AB是⊙O的直径，EF，EB是⊙O的弦，且EF=EB，EF与AB交于点C，连接OF，若∠AOF=40°，则∠F的度数是（）

A . 20° B . 35° C . 40° D . 55°

答案解析收藏纠错 + 选题
8. (2024九上·青县月考) 下表中列出的是一个二次函数的自变量x与函数y的几组对应值：

$\text{[math]}$

…

-2

0

1

3

…

$\text{[math]}$

…

6

-4

-6

-4

…

下列各选项中，正确的是

A . 这个函数的图象开口向下 B . 这个函数的图象与x轴无交点 C . 这个函数的最小值小于-6 D . 当 $\text{[math]}$ 时，y的值随x值的增大而增大

答案解析收藏纠错 + 选题

二、填空题

9. (2022·陕西模拟) 分解因式：2 $\text{[math]}$ ＝.

答案解析收藏纠错 + 选题
10. (2022·陕西模拟) 我国战国时期提出“一尺之棰，日取其半，万世不竭”这一命题，用所学知识来解释可理解为：设一尺长的木棍，第一天折断一半，其长为 $\text{[math]}$ 尺，第二天再折断一半，其长为 $\text{[math]}$ 尺，…，第n天折断一半后得到的木棍长应为尺.

答案解析收藏纠错 + 选题
11. (2024八上·阳泉期末) 如图，在正五边形ABCDE中，DM是边CD的延长线，连接BD，则∠BDM的度数是.

答案解析收藏纠错 + 选题
12. (2022·陕西模拟) 如图，在Rt△OAB中，∠OAB＝90°，OA＝6，AB＝4，边OA在x轴上，若双曲线 $\text{[math]}$ 经过边OB上一点D（4，m），并与边AB交于点E，则点E的坐标为.

答案解析收藏纠错 + 选题
13. (2022·陕西模拟) 如图，在菱形 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点O， $\text{[math]}$ 于点E，F是 $\text{[math]}$ 的中点，P是 $\text{[math]}$ 边上的一个动点，则 $\text{[math]}$ 的最大值是.

答案解析收藏纠错 + 选题

三、解答题

14. (2022·陕西模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2022·陕西模拟) 解不等式组： $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2022·陕西模拟) 解方程： $\text{[math]}$ .

答案解析收藏纠错 + 选题
17. (2022·陕西模拟) 如图，在△ABC中，AB=AC，AD是BC边上的高。请用尺规作图法，求作△ABC的外接圆。（保留作图痕迹，不写做法）

答案解析收藏纠错 + 选题
18. (2023八下·自贡期末) 如图，在四边形ABCD中，AD∥BC，∠B＝∠C.E是边BC上一点，且DE＝DC.求证：AD＝BE.

答案解析收藏纠错 + 选题
19. (2022·陕西模拟) 为了适应新的教育形势发展的需要，某初中学校研究决定探索符合学校情况的课改模式，通过多方面调查、探究和思考，学校最终确定的课改思路为“先学后教、以学定教”，根据学校实际，决定先在七年级实行小班教学，但学校能供七年级用的教室有限，若每间教室安排40名学生，则缺少1间教室；若每间教室安排44名学生，则空出1间教室，问：该校能供七年级学生所用的教室共有多少间？

答案解析收藏纠错 + 选题
20. (2023八下·江源期末) 王大伯承包了一个鱼塘，投放了2000条某种鱼苗，经过一段时间的精心喂养，存活率大致达到了90%.他近期想出售鱼塘里的这种鱼.为了估计鱼塘里这种鱼的总质量，王大伯随机捕捞了20条鱼，分别称得其质量后放回鱼塘.现将这20条鱼的质量作为样本，统计结果如图所示：
1. （1）这20条鱼质量的中位数是，众数是.
2. （2）求这20条鱼质量的平均数；
3. （3）经了解，近期市场上这种鱼的售价为每千克18元，请利用这个样本的平均数.估计王大伯近期售完鱼塘里的这种鱼可收入多少元？
答案解析收藏纠错 + 选题
21. (2022·陕西模拟) 如图，学校一幢教学楼 $\text{[math]}$ 的顶部竖有一块写有校训的宣传牌 $\text{[math]}$ ，小同在M点用测倾器测得宣传牌的底部A点的仰角为 $\text{[math]}$ ，他向教学楼前进7米到达N点，测得宣传牌顶部 $\text{[math]}$ 点的仰角为 $\text{[math]}$ ，已知广告牌 $\text{[math]}$ 的高度为3米，测倾器 $\text{[math]}$ 米，点B、M、N在同一水平面上，不考虑其他因素，求教学楼 $\text{[math]}$ 的高度.（结果保留整数，参考数据 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

答案解析收藏纠错 + 选题
22. (2022·陕西模拟) 龟、兔进行了一次900米赛跑，如图表示龟兔赛跑的路程s（米）与时间t（分钟）的关系，根据图象回答以下问题：
1. （1）在此次比赛过程中，兔子中途睡了分钟；
2. （2）求 $\text{[math]}$ 的函数表达式；
3. （3）乌龟到终点时，兔子距离终点还有多远.
答案解析收藏纠错 + 选题

23. (2022·陕西模拟) 一个不透明的袋子中装有1个黄球和若干个蓝球，这些球除颜色外重量、大小、表面光滑度等都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回；搅匀后再摸一个球，记下颜色后放回；不断重复这个过程，获得数据如下：

摸球的次数	100	200	300	400	500
摸到黄球的频数	26	51	75	98	126
摸到黄球的频率	0.260	0.255	0.250	0.245	0.252

（1）该学习小组发现，摸到黄球的频率在一个常数附近摆动，这个常数是（精确到0.01），由此估出蓝球有个；
（2）现从该袋中一次摸出2个球，请用树状图或列表的方法列出所有等可能的结果，并求恰好摸到1个黄球，1个蓝球的概率.

答案解析收藏纠错 + 选题

24. (2022·陕西模拟) 如图，AB是⊙O的直径，AC是⊙O的切线，且CA=BA.连接BC，OC.过点A作AD⊥OC于点D，延长AD交BC于点E，交⊙O于点F，连接BF.
1. （1）求证：∠FAB=∠ACD；
2. （2）若BF=4，求DE的长.
答案解析收藏纠错 + 选题
25. (2022·陕西模拟) 已知抛物线L： $\text{[math]}$ 过点 $\text{[math]}$ 和 $\text{[math]}$ ，与x轴的交点为A、B（点A在点B的左侧）.
1. （1）求抛物线L的表达式；
2. （2）若点P在抛物线L上，点E、F在抛物线L的对称轴上，D是抛物线L的顶点，要使 $\text{[math]}$ （P的对应点是D），且 $\text{[math]}$ .求满足条件的点P的坐标.
答案解析收藏纠错 + 选题
26. (2022·陕西模拟)
1. （1）问题提出：如图1，已知△ABC，试确定一点D，使得以A，B，C，D为顶点的四边形为平行四边形，请画出这个平行四边形；
2. （2）问题探究：
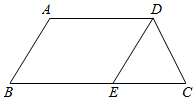
  如图2，在矩形ABCD中，AB=4，BC=10，若要在该矩形中作出一个面积最大的△BPC，且使∠BPC＝90°，求满足条件的点P到点A的距离；
3. （3）问题解决：
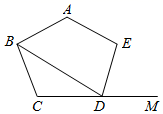
  如图3，有一座草根塔A，按规定，要以塔A为对称中心，建一个面积尽可能大的形状为平行四边形的草根景区BCDE.根据实际情况，要求顶点B是定点，点B到塔A的距离为50米，∠CBE=120°，那么，是否可以建一个满足要求的面积最大的平行四边形景区BCDE？若可以，求出满足要求的平行四边形BCDE的最大面积；若不可以，请说明理由.（塔A的占地面积忽略不计）
答案解析收藏纠错 + 选题