班级 | 参加人数 | 中位数 | 方差 | 平均数 |
甲 | 40 | 129 | 161 | 115 |
乙 | 40 | 131 | 90 | 115 |
某同学分析上表后得到如下结论:
①甲、乙两班学生平均成绩相同;
②乙班优秀的人数多于甲班优秀的人数(每分跳绳个数为优秀);
③甲班成绩的波动比乙班大.
上述结论正确的是( )


下面四个推断:
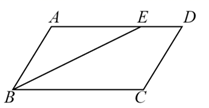
①四边形ABFM是平行四边形;
②四边形ENFM是平行四边形;
③若▱ABCD是矩形(正方形除外),则至少存在一个四边形ENFM是正方形;
④对于任意的▱ABCD,存在无数个四边形ENFM是矩形.
其中,正确的有.
![]()
求作:菱形ABCD,使其一条对角线的长等于线段a的长,边长等于线段b的长.
作法:①作直线m,在m上截取线段;
②作线段AC的垂直平分线EF,交线段AC于点O;
③以点A为圆心,线段b的长为半径画弧,交直线EF于点B,D;
④分别连接AB,BC,CD,DA;
则四边形ABCD就是所求作的菱形.
![]()
证明:∵EF垂直平分AC,
∴AB= ▲ , ▲ = ▲ , ( )
∵ ,
,
∴四边形ABCD是菱形.( )
a.30名同学测试成绩的统计图如下:

b.30名同学测试成绩的频数分布直方图如下(数据分成6组: ,
,
,
,
,
):
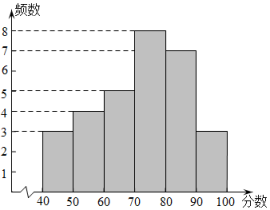
c.测试成绩在这一组的分别是:
73 74 77 75 70 74 73 78
d.小华的知识测试成绩为85分.
根据以上信息,回答下列问题:
通过上面三个计算,可以初步对任意的非负实数a,b做出猜想:
;




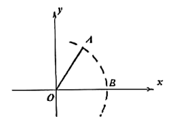
①线段OF的最小值为,最大值为;线段DF的取值范围是;
②在点O,D中,点与线段CE满足限距关系;


