（人教版）2021-2022学年度第二学期八年级数学第19章...

更新时间：2022-05-27 浏览次数：114 类型：复习试卷

一、单选题

1. (2022七下·诏安期中) 弹簧挂上物体后会伸长，测得一弹簧的长度y（cm）与所挂的物体的质量x（kg）间有下面的关系：
x/kg
0
1
2
3
4
5
y/cm
10
10.5
11
11.5
12
12.5
下列说法一定错误的是（）

A . x与y都是变量，且x是自变量，y是因变量 B . 弹簧不挂重物时的长度为0cm C . 物体质量每增加1kg，弹簧长度y增加0.5 cm D . 所挂物体质量为7kg时，弹簧长度为13.5cm

答案解析收藏纠错 + 选题
2. (2022·芜湖模拟) 下列函数中，图象经过原点的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021八上·广南期末) 下列各图中，不能表示y是x的函数的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021八上·松江期末) 已知正比例函数 $\text{[math]}$ 的图像经过点（2， $\text{[math]}$ 4）、（1， $\text{[math]}$ ）、（ $\text{[math]}$ 1， $\text{[math]}$ ），那么 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法确定

答案解析收藏纠错 + 选题
5. (2021八上·松江期中) 点 $\text{[math]}$ 、点 $\text{[math]}$ 在正比例函数 $\text{[math]}$ 的图像上，当 $\text{[math]}$ 时，则 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 无法判断

答案解析收藏纠错 + 选题
6. (2021八上·牡丹期中) 对于函数 $\text{[math]}$ （k是常数， $\text{[math]}$ ），下列说法错误的是（）

A . 该函数是正比例函数 B . 该函数图象过 $\text{[math]}$ C . 该函数图象经过二、四象限 D . y随着x的增大而增大

答案解析收藏纠错 + 选题
7. (2022九下·汕头期末) 如图，一束光线从点A（4，4）发出，经y轴上的点C反射后，经过点B（1，0），则点C的坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022八下·开福期中) 已知一次函数 $\text{[math]}$ 的图象如图，则不等式 $\text{[math]}$ 的解集为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·蒙阴模拟) 直线y=﹣2x﹣1关于y轴对称的直线与直线y=﹣2x+m的交点在第四象限，则m的取值范围是（）

A . m>﹣1 B . m<1 C . ﹣1<m<1 D . ﹣1≤m≤1

答案解析收藏纠错 + 选题
10. (2022九下·重庆开学考) 春节前，某加工厂接到面粉加工任务，要求5天内加工完220吨面粉.加工厂安排甲、乙两组共同完成加工任务.乙组加工中途停工一段时间维修设备，然后提高加工效率继续加工，直到与甲队同时完成加工任务为止.设甲、乙两组各自加工面粉数量y（吨）与甲组加工时间x（天）之间的关系如图所示，结合图象，下列结论错误的是（）

A . 乙组中途休息了1天 B . 甲组每天加工面粉20吨 C . 加工3天后完成总任务的一半 D . 3.5天后甲乙两组加工面粉数量相等

答案解析收藏纠错 + 选题

二、填空题

11. (2021七上·锡山期中) 某市地铁票价计费标准如表所示：乘车距离x(单位：公里)：

乘车距离x	x≤6	6＜x≤12	12＜x≤22	22＜x≤32	x＞32
票价（元）	3	4	5	6	每增加1元可乘20公里

另外，使用市政交通一卡通，每个自然月每张卡片支出累计满100元后，超出部分打8折；满150元后，超出部分打5折；支出累计达400元后，不再打折.小红妈妈上班时，需要乘坐地铁15公里到达公司，每天上下班共乘坐两次，如果每次乘坐地铁都使用市政交通一卡通，那么每月第22次乘坐地铁上下班时，她刷卡支出的费用是元.

答案解析收藏纠错 + 选题

12. (2021八上·徐汇期末) 已知正比例函数 $\text{[math]}$ 的图象经过第一、三象限，且经过点（k，k+2），则k=．

答案解析收藏纠错 + 选题
13. (2022·南开模拟) 已知一次函数 $\text{[math]}$ 的图象向上平移b个单位后经过第一象限，请你写出一个符合条件的b的值为．

答案解析收藏纠错 + 选题
14. (2022八下·东台开学考) 如图，函数y＝2x和y＝ax+4的图象相交于点A（n，2），则不等式2x≥ax+4的解集为．

答案解析收藏纠错 + 选题
15. (2021七上·肇源期末) 河北给武汉运送抗疫物资，某汽车油箱内剩余油量Q（升）与汽车行驶路程s（千米）有如下关系：
行驶路程s（千米）
0
50
100
150
200
…
剩余油量Q（升）
40
35
30
25
20
…
则该汽车每行驶100千米的耗油量为升．

答案解析收藏纠错 + 选题

三、解答题

16. 物体从高处自由下落的高度h(m)与物体下落的时间t(s)之间的函数关系式是：h＝ $\text{[math]}$ gt²(g表示重力加速度，g取9.8m/s²)．某人发现头顶上空490m处有一炸弹自由下落，其地面杀伤半径为50m，此人发现后，立即以6m/s的速度逃离，那么此人有无危险？

答案解析收藏纠错 + 选题
17. (2019八上·银川期中) 请在图中画出直线 $\text{[math]}$ 的图象，并且直线与 $\text{[math]}$ 轴、 $\text{[math]}$ 轴交点分别为 $\text{[math]}$ ，若直线 $\text{[math]}$ 上的点 $\text{[math]}$ 在第一象限，且 $\text{[math]}$ ，求点 $\text{[math]}$ 的坐标.

答案解析收藏纠错 + 选题
18. 已知正比例函数y=kx经过点A，点A在第四象限，过点A作AH⊥x轴，垂足为点H，点A的横坐标为3，且△AOH的面积为3．
（1）求正比例函数的解析式；
（2）在x轴上能否找到一点P，使△AOP的面积为5？若存在，求点P的坐标；若不存在，请说明理由．

答案解析收藏纠错 + 选题
19. (2021八上·吉安期中) 已知 $\text{[math]}$ 与 $\text{[math]}$ 成正比例，且当 $\text{[math]}$ 时， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数表达式；
2. （2）当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
20. (2021九上·太原月考) 在平面直角坐标系中，直线 $\text{[math]}$ ： $\text{[math]}$ 分别与x轴、y轴交于点A、点B，且与直线 $\text{[math]}$ ： $\text{[math]}$ 于点C．
$\text{[math]}$ Ⅰ $\text{[math]}$ 如图 $\text{[math]}$ ，求出B、C两点的坐标；

$\text{[math]}$ Ⅱ $\text{[math]}$ 若D是线段OC上的点，且 $\text{[math]}$ 的面积为4，求直线BD的函数解析式．

$\text{[math]}$ Ⅲ $\text{[math]}$ 如图 $\text{[math]}$ ，在 $\text{[math]}$ Ⅱ $\text{[math]}$ 的条件下，设P是射线BD上的点，在平面内是否存在点Q，使以O、B、P、Q为顶点的四边形是菱形？若存在，直接写出点Q的坐标；若不存在，请说明理由．

答案解析收藏纠错 + 选题
21. (2021八下·南开期末) 如图，直线 $\text{[math]}$ 分别与x轴，y轴交于A､B两点，A､B的坐标分别为 $\text{[math]}$ 、 $\text{[math]}$ ，过点B的直线 $\text{[math]}$ 交x轴于点C ，点 $\text{[math]}$ 是直线l上的一点，连接 $\text{[math]}$ ．

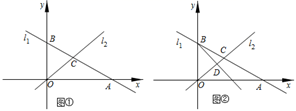
（Ⅰ）求 $\text{[math]}$ 的解析式；

（Ⅱ）求C､D的坐标；

（Ⅲ）求 $\text{[math]}$ 的面积．

答案解析收藏纠错 + 选题
22. (2019八上·太原期中) 如图，已知一次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴， $\text{[math]}$ 轴分别交于A，B两点，点 $\text{[math]}$ 在该函数的图象上，连接OC．求点A，B的坐标和 $\text{[math]}$ 的面积.

答案解析收藏纠错 + 选题
23. (2021·阳西模拟) 某校积极响应国家号召，为落实垃圾“分类回收，科学处理”的政策，准备购买 $\text{[math]}$ L和 $\text{[math]}$ L两种型号的垃圾箱若干套．若购买8套 $\text{[math]}$ L垃圾箱和5套 $\text{[math]}$ L垃圾箱，共需7200元；若购买4套 $\text{[math]}$ L垃圾箱和6套 $\text{[math]}$ L垃圾箱，共需6400元．
1. （1）每套 $\text{[math]}$ L垃圾箱和每套 $\text{[math]}$ L垃圾箱各多少元？
2. （2）学校决定购买 $\text{[math]}$ L垃圾箱和 $\text{[math]}$ L垃圾箱共20套，且 $\text{[math]}$ L垃圾箱的数量不少于 $\text{[math]}$ L垃圾箱数量的 $\text{[math]}$ ，求购买这20套垃圾箱的最少费用．
答案解析收藏纠错 + 选题