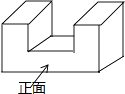
 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 

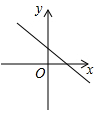 B .
B .  C .
C . 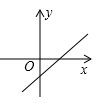 D .
D . 


并给出了部分信息:
【一】七年级D等级的学生人数占七年级抽取人数的20%,
八年级C等级中最低的10个分数分别为:
73,70,75,70,74,75,72,73,73,74
【二】两个年级学生防自然灾害知识测评分数统计图:

污水处理设备 | A型 | B型 |
价格(万元/台) | m | m﹣3 |
月处理污水量(吨/台) | 2200 | 1800 |
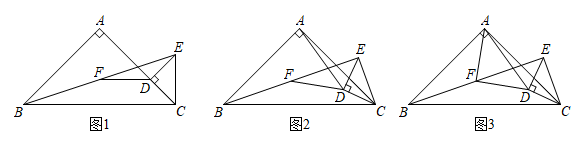
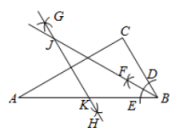
①如图2,(1)中∠ADF的度数及线段AD与DF的数量关系是否仍然成立?请说明理由;
②如图3,连接AF,若AC=3,CD=1,求S△ADF的取值范围.