


 B .
B .  C .
C .  D .
D . 
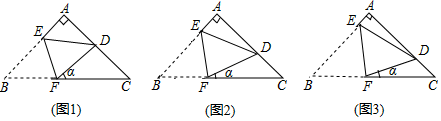
如图,当 时,
;
如图,当 时,
;
如图,当 时,
;
……
依此类推,当 (
为正整数)时,
.
A | 经典诵读与写作 |
B | 数学兴趣与培优 |
C | 英语阅读与写作 |
D | 艺体类 |
E | 其他 |
为了了解学生的选择情况(每名学生均按要求选择了其中一项),现从该校随机抽取了部分学生进行问卷调查,并根据调查得到的数据绘制了如图所示的两幅不完整的统计图.请根据统计图提供的信息回答下列问题:

(参考数据: ,
,
)

方案一 | 方案二 | ||
购进数量(本) | 甲种图书 | 600 | 400 |
乙种图书 | 600 | 800 | |
售完后总收入(元) | 28800 | 27200 | |
设长方形中,
,
.



探究1:设每个小正方形的边长均为1.
①如图2,在长方形中,
,
. 若小球从格点O出发,依次在
、
、
边上经过3次反弹后恰好回到点O,显然,此时
.
②如图3,在长方形中,
,
. 若小球从格点O出发,依次在
、
、
边上经过3次反弹后恰好回到点O,显然,此时
.
③如图4,在长方形中,
,
, 若小球从格点O出发,依次在
、
、
边上经过3次反弹后恰好回到点O,请在图3中用
、
、
标记每条边上的反弹点,并画出小球每次反弹的轨迹,再直接写出此时k=…….
……
通过归纳,时,k与x、y间的等量关系为:.
当时,有图5、图6两种情况.请直按写出k与x、y之间所有可能的等量关系:.
②请直接写出当时,k与x、y之间所有可能的等量关系:.
若长方形中,k为该长方形的n次完美反弹比(
且n为奇数),请直接写出k与n、x、y之间所有可能的等量关系:.
