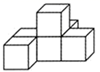
 B .
B . 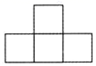 C .
C . 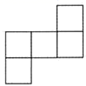 D .
D . 



![]()
①当时,
;
②当时,若a为奇数,且
, 则
或5;
③若 ,
, 则
;
④当 ,
时,将点B水平右移3个单位至点
, 再将点
水平右移3个单位至点
, 以此类推,…且满足
, 则数轴上与
对应的点
表示的数为
.


证明:设AE交DF于点T.
在正方形ABCD中,DA=AB,
∠DAF=∠B=90°,
又∵
∴△DAF≌△
∴ , .
∵∠BAE+∠DAT=90°,∴∠ADF+∠DAT=90°.∴∠ATD=90°.
∴AE⊥DF,∴AE=DF,AE⊥DF.
并给出了部分信息:
【一】七年级D等级的学生人数占七年级抽取人数的20%,
八年级C等级中最低的10个分数分别为:70,70,72,73,73,73,74,74,75,75.
【二】两个年级学生防自然灾害知识测评分数统计图:

【三】两个年级学生防自然灾害知识测评分数样本数据的平均数、中位数、众数如下:
平均数 | 中位数 | 众数 | |
七年级 | 76 | 75 | 73 |
八年级 | 76 | a | 72 |

材料二:若t=(1≤a≤9,0≤b≤9,0≤c≤9,且a,b,c均为整数),记F(t)=2a﹣c.
