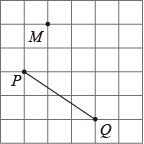
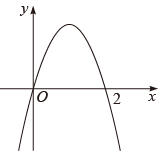
 B .
B .  C .
C .  D .
D . 
学生序号 | 1 | 2 | 3 | 4 | 5 | 6 |
身高差值(cm) | +2 | x | +3 | ﹣1 | ﹣4 | ﹣1 |
据此判断,2号学生的身高为 cm.
参考数据:sin22°≈ , cos22°≈
, tan22°≈
, sin67°≈
, cos67°≈
, tan67°≈
.
平均每天阅读时间统计表
等级 | 人数(频数) |
A(10≤m<20) | 5 |
B(20≤m<30) | 10 |
C(30≤m<40) | x |
D(40≤m<50) | 80 |
E(50≤m≤60) | y |

请根据图表中的信息,解答下列问题:
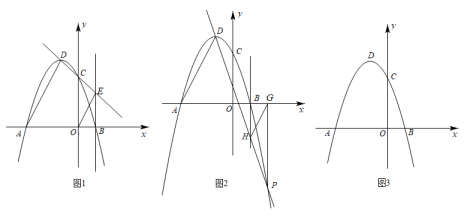
①如图1,直线DC交直线x=1于点E,连接OE.求证:AD∥OE;
②如图2,点P(2,﹣5)为抛物线y=ax2+bx+3(a≠0)上一点,过点P作PG⊥x轴,垂足为点G.直线DP交直线x=1于点H,连接HG.求证:AD∥HG;
猜想:作MN⊥x轴于N,直线DM交直线x=1于Q,则QN∥AD,证明见解析
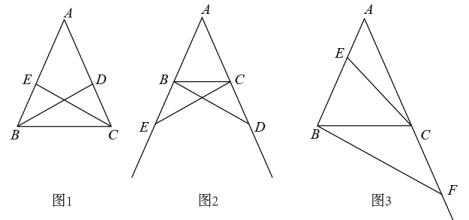
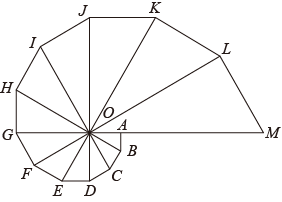
①BD,CE是△ABC的角平分线.求证:BD=CE.
②点D,E分别是边AC,AB的中点,连接BD,CE.求证:BD=CE.
(从①②两题中选择一题加以证明)
经过做题反思,小明同学认为:在△ABC中,AB=AC,D为边AC上一动点(不与点A,C重合).对于点D在边AC上的任意位置,在另一边AB上总能找到一个与其对应的点E,使得BD=CE.进而提出问题:若点D,E分别运动到边AC,AB的延长线上,BD与CE还相等吗?请解决下面的问题:
如图2,在△ABC中,AB=AC,点D,E分别在边AC,AB的延长线上,请添加一个条件(不再添加新的字母),使得BD=CE,并证明.
如图3,在△ABC中,AB=AC=2,∠A=36°,E为边AB上任意一点(不与点A,B重合),F为边AC延长线上一点.判断BF与CE能否相等.若能,求CF的取值范围;若不能,说明理由.