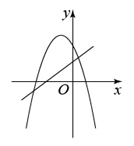 B .
B .  C .
C . 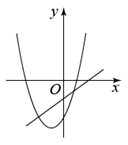 D .
D . 
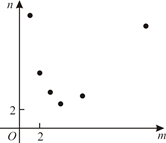 B .
B . 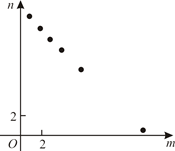 C .
C . 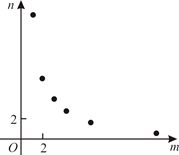 D .
D . 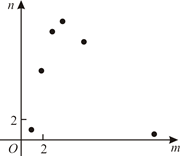
|
|
5 |
… |
|
… |
… |
… |
|
… |
1 |
|
|
20 |
30 |
40 |
50 |
60 |
70 |
80 |
90 |
100 |

 B .
B .  C .
C .  D .
D . 