河北省石家庄市2023-2024学年九年级下学期数学开学考试...

更新时间：2024-05-07 浏览次数：24 类型：开学考试

一、选择题（本大题共16个小题，共38分、1-6小题各3分，7-16小题各2分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2024九下·石家庄开学考) 一个有理数与﹣2相加的和为2，则这个有理数是（　　）

A . 0 B . 1 C . 4 D . ﹣4

答案解析收藏纠错 + 选题
2. (2024八上·沅江开学考) 如图，将三角形纸片折叠，使点B ， C重合，折痕DE与AB ， BC分别交于点D、点E ，连接AE ，下列是△ABC的中线的是（　　）

A . 线段AE B . 线段BE C . 线段CE D . 线段DE

答案解析收藏纠错 + 选题
3. (2024七下·竞秀期中) 若 $\text{[math]}$ ，则“□”内应填的运算符号为（　　）

A . + B . ﹣ C . × D . ÷

答案解析收藏纠错 + 选题
4. (2024九下·石家庄开学考) 如图，人字梯的支架AB ， AC的长度都为2m（连接处的长度忽略不计），则B、C两点之间的距离可能是（　　）

A . 3m B . 4.2m C . 5m D . 6m

答案解析收藏纠错 + 选题
5. (2024八下·河池期中) 与 $\text{[math]}$ 的结果不相等的是（　　）

A . $\text{[math]}$ B . 2×3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024九下·石家庄开学考) 如图的几何体是由10个相同的小正方体搭成的，若移走下列中的一块小正方体后，该几何体的主视图会发生改变，则可能移走的是（　　）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题
7. (2024七下·永善期中) 老师在黑板上画出如图所示的图形，要求学生添加条件，使得AB∥CD ，随后抽取了四名学生的答案纸展示如下：
甲：∠B+∠BCD＝180°；
乙：∠1＝∠2；
丙：∠B＝∠DCE；
丁：∠3＝∠4．
则不能得到AB∥CD的是（　　）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
8. (2024九下·石家庄开学考) 将一个数用科学记数法表示成a×10ⁿ的形式，关于a和n的值，下列说法不正确的是（　　）

A . a的值一定小于10 B . a的值可能是0.25 C . n的值一定是整数 D . n的值可能是负整数

答案解析收藏纠错 + 选题
9. (2024九下·石家庄开学考) 若a ， b互为倒数，则分式 $\text{[math]}$ 的值为（　　）

A . 1 B . 0 C . ﹣1 D . ﹣2

答案解析收藏纠错 + 选题
10. (2024八下·道县月考) 如图，已知△ABD ，用尺规进行如下操作：①以点B为圆心，AD长为半径画弧；②以点D为圆心，AB长为半径画弧；③两弧在BD上方交于点C ，连接BC ， DC ．可直接判定四边形ABCD为平行四边形的条件是（　　）

A . 两组对边分别平行 B . 两组对边分别相等 C . 对角线互相平分 D . 一组对边平行且相等

答案解析收藏纠错 + 选题
11. (2024九下·石家庄开学考) 如图，△ABC绕点C旋转得到△DEC ，且点E在边AB上，M为AC与DE的交点．若∠BCE＝25°，则下列各角：①∠ACD；②∠AED；③∠ACE；④∠BAC ．其中角的度数一定等于25°的是（　　）

A . ①② B . 只有① C . ③④ D . ②③

答案解析收藏纠错 + 选题
12. (2024九下·石家庄开学考) 对于任意自然数n ，关于代数式（n+7）²﹣（n﹣5）²的值，说法错误的是（　　）

A . 总能被3整除 B . 总能被4整除 C . 总能被6整除 D . 总能被7整除

答案解析收藏纠错 + 选题
13. (2024九下·石家庄开学考) 如图，在Rt△ABC中，点M是斜边BC的中点，以AM为边作正方形AMEF ，下列三角形中，外心不是点M的是（　　）

A . △ABC B . △AEC C . △ACF D . △BCE

答案解析收藏纠错 + 选题
14. (2024九下·石家庄开学考) 某市举行中学生党史知识竞赛，如图用四个点分别描述甲、乙、丙、丁四所学校竞赛成绩的优秀率（该校优秀人数与该校参加竞赛人数的比值） $\text{[math]}$ 与该校参加竞赛人数 $\text{[math]}$ 的情况，其中描述乙、丁两所学校情况的点恰好在同一个反比例函数的图象上，则这四所学校在这次党史知识竞赛中成绩优秀人数最多的是（）

A . 甲 B . 乙 C . 丙 D . 丁

答案解析收藏纠错 + 选题
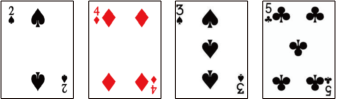
15. (2024九下·石家庄开学考) 有4张扑克牌如图所示，将其背面朝上，打乱顺序后放在桌面上．若从中随机抽取两张，则抽到的花色均为♠（黑桃）的概率为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2024九下·石家庄开学考) 如图，等边△ABC的边长为5，点D ， P ， L分别在边AB ， BC ， CA上，AD＝BP＝CL＝x（x＞0），按如图方式作边长均为3的等边△DEF ， △PQR ， △LMN ，点F ， R ． N分别在射线DA ， PB ， LC上．
结论Ⅰ：当边DE ， PQ ， LM与△ABC的三边围成的图形DGPHLI是正六边形时，x＝1；
结论Ⅱ：当点D与点B重合时，EF ， QR ， MN围成的三角形的周长为3．
针对结论Ⅰ和Ⅱ，下列判断正确的是（　　）

A . Ⅰ和Ⅱ都对 B . Ⅰ和Ⅱ都不对 C . Ⅰ不对Ⅱ对 D . 1对Ⅱ不对

答案解析收藏纠错 + 选题

二、填空题（本大题共3个小题，共10分，17小题2分，18～19小题各4分，每空2分）

17. (2024九下·石家庄开学考) 如图，数轴上的两个点分别表示﹣3和m ，请写出一个符合条件的m的整数值：．

答案解析收藏纠错 + 选题
18. (2024九下·石家庄开学考) 某面粉加工厂加工甲、乙两种颗粒面粉，每天共加工两种面粉100袋，相关信息如下表：

成本（元/袋）
售价（元/袋）
甲
30
43
乙
28
36
设每天生产甲种颗粒面a袋．
1. （1）每天加工甲、乙两种颗粒面的总成本为元（用含a的代数式表示）；
2. （2）当a＝60时，每天加工甲、乙两种颗粒面的总利润为元．（利润＝售价﹣成本）
答案解析收藏纠错 + 选题
19. (2024九下·石家庄开学考) 如图，点A（3，0），B（0，4），连接AB ，点D为x轴上点A左侧的一点，点E ， F分别为线段AB ，线段BO上的点，点B ， D关于直线EF对称．
1. （1）若DE⊥AO ，则四边形BEDF的形状是；
2. （2）当AD最长时，点F的坐标为．
答案解析收藏纠错 + 选题

三、解答题（本大题共7个小题，共72分.解答应写出文字说明、证明过程或演算步骤）

20. (2024九下·石家庄开学考) 老师在黑板上写下“3①3②”，其中①、②分别是0～9之间的一个数字，但不能重复，进行填数游戏．老师提出了以下问题，请你完成：
1. （1）当“3①3②”最小时，计算①﹣3+②﹣3的值；
2. （2）若“3①3②”比“3②3①”大396、且①、②中的一个数是另一个数的2倍，求①、②所代表的数字．
答案解析收藏纠错 + 选题
21. (2024九下·石家庄开学考) 为适应现代快节奏生活，利用外卖平台购买餐食已经成为很普通的一件事，某饼屋利用外卖平台进行销售餐食．饼屋根据10月9日﹣13日饼类的外卖平台销售情况绘制了不完整的统计图（如图1）和统计表，日增长率＝ $\text{[math]}$ ×100%．
10月9日﹣13日饼类外卖销售日增长统计表
日期/日
日增长率（精确到1%）
9
无
10
50%
11
m
12
﹣15%
13
10%
（负数表示减少的百分数）
请根据以上信息解答下列问题：
1. （1） m＝，并补全图1的条形统计图；
2. （2）求饼屋日销售量的中位数，以及从10日至13日饼屋销售量的日增长率的平均数．
答案解析收藏纠错 + 选题
22. (2024九下·石家庄开学考) 如图1是边长分别为m ， n、p的A、B、C三种正方形．
1. （1）用两个A种正方形组合成图2的图形，外边框可以围成一个大正方形，则这个大正方形的面积＝（用含m的代数式表示）；
2. （2）将一个A种和一个B种正方形组合成图3的图形，外边框可以围成一个大正方形，用两种不同的方法表示这个大正方形的面积：或；则根据这个大正方形面积的不同表示方法，可以得到的乘法公式为；
3. （3）将A种、B种和C种正方形组合形成图4的图形，此时的外边框可以围成一个大的正方形，根据（2）中乘法公式的生成过程，直接写出所得到的等式，并令m＝1，n＝3，p＝2，通过计算验证该等式．
答案解析收藏纠错 + 选题
23. (2024九下·石家庄开学考) 如图，直线l₁与x轴交于点A（5，0），与y轴交于点B（0，5），直线l₂的解析式为y＝3x﹣3．
1. （1）求直线l₁的解析式；
2. （2）求直线l₁被直线l₂和y轴所截线段的长．
答案解析收藏纠错 + 选题
24. (2024·南京二模) 筒车是我国古代利用水力驱动的灌溉工具，如图，半径为3m的筒车⊙O按逆时针方向每分钟转 $\text{[math]}$ 圈，筒车与水面分别交于点A、B ，筒车的轴心O距离水面的高度OC为2.2m ，筒车上均匀分布着若干个盛水筒，若以某个盛水筒P刚浮出水面（点A）时开始计算时间．
1. （1）求盛水筒P从A点到达最高点所经过的路程；
2. （2）求浮出水面3.4秒时，盛水筒P到水面的距离；
3. （3）若接水槽MN所在直线是⊙O的切线，且与直线AB交于点M ， MO＝8m ，直接写出盛水筒P从最高点开始，经过多长时间恰好第一次落在直线MN上．（参考数据：cos43°＝sin47°≈ $\text{[math]}$ ， sin16°＝cos74°≈ $\text{[math]}$ ， sin22°＝cos68°≈ $\text{[math]}$ ）
答案解析收藏纠错 + 选题
25. (2024九下·深圳月考) 某排球运动员在原点O处训练发球，MN为球网，AB为球场护栏，且MN ， AB均与地面垂直，球场的边界为点K ，排球（看作点）从点O的正上方点P（0，2）处发出，排球经过的路径是抛物线L的一部分，其最高点为G ，落地点为点H ，以点O为原点，点O ， M ， H ， K ， A所在的同一直线为x轴建立平面直角坐标系，相应点的坐标如图所示，点N的坐标为（9，2.4）（单位：米，图中所有的点均在同一平面内）．
1. （1）求抛物线L的函数表达式；
2. （2）通过计算判断发出后的排球能否越过球网？是否会出界？
3. （3）由于运动员作出调整改变了发球点P的位置，使得排球在点K落地后立刻弹起，又形成了一条与L形状相同的抛物线L^' ，且最大高度为1m ．若排球沿L^'下落时（包含最高点）能砸到球场护栏AB ，直接写出m的最大值与最小值的差．
答案解析收藏纠错 + 选题
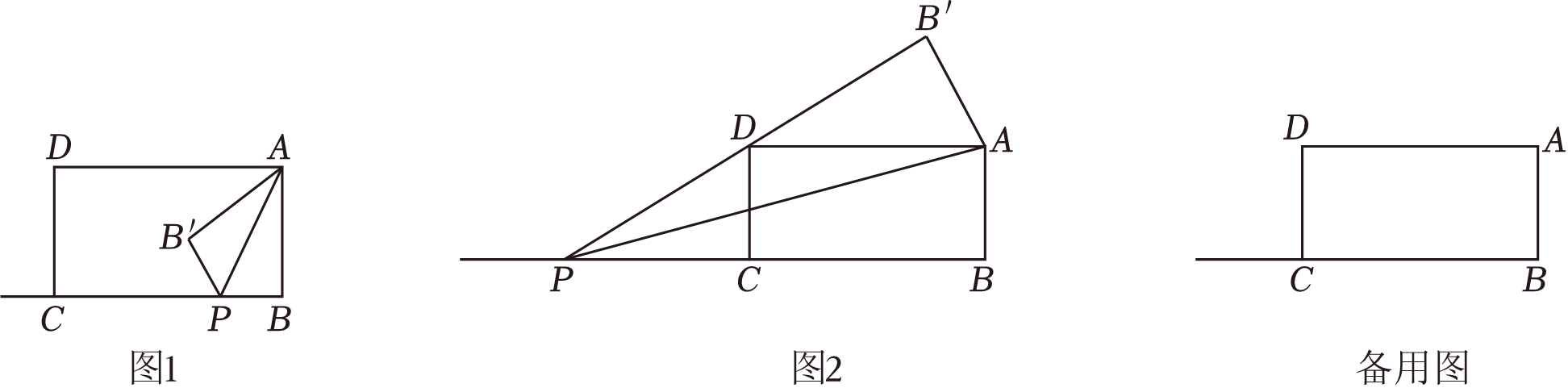
26. (2024九下·石家庄开学考) 如图1和图2，在矩形ABCD中，AB＝6，BC＝12，将线段AB绕点A顺时针旋转n°（0＜n＜180）到AB'，∠BAB^'的平分线AP交射线BC于点P ，连接B^'P ，设BP＝x ，
1. （1）求证：BP＝B^'P；
2. （2）如图2，当B^'P经过点D时，n＝，求x的值；
3. （3）在线段AB绕点A旋转过程中：
  ①当点B^'到AD的距离为2时，求x的值；
  ②直接写出点B^'到射线BC的距离（用含x的式子表示）．
答案解析收藏纠错 + 选题