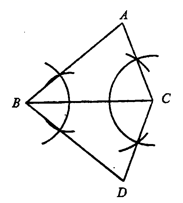

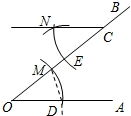


第一步:尺规作图.
作法:(1)作射线M;(2)以点B为圆心,任意长为半径画弧,分别交BA,BC于点E,D;(3)以点
为圆心,BD长为半径画弧,交
M于点P;(4)以点P为圆心,DE长为半径画弧,在
M的上方交(3)中所画弧于点Q;(5)过点Q作射线BˊN;(6)以点
为圆心,BC长为半径画弧,交
M于点
;(7)以点
为圆心,BA长为半径画弧,交
N于点
;(8)连接
.
第二步:把作出的剪下来,放到
上.
第三步:观察发现和
重合.
∴ .
根据小举的操作过程可知,小举是在探究( )
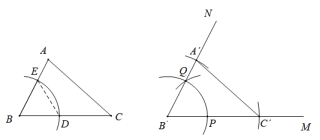





作法如下:
①连接 ,作
的垂直平分线分别交直线
于点
,连接
,则
;
②过点D作 的平行线交
于点P , 在线段
上截取
,使
,连接
,则
;
③过点D作 的平行线交
于点P , 过点D作
的平行线交
于点Q , 连接
,则
;
④过点D作 的平行线交
于点Q , 在直线
上取一点P , 连接
,使
,连接
,则
.以上说法一定成立的是.(填写正确的序号)
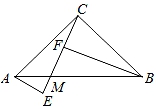

①如图2,当点D在线段BC上移动时,α,β之间有怎样的数量关系?请说明理由。
②当点D在直线BC上移动时,α,β之间有怎样的数量关系?请你在备用图上画出图形,并直接写出结论。


①如图3,当点 在线段
上移动,则
,
之间有怎样的数量关系?请说明理由;

②当点 在直线
上移动,请直接写出
,
之样的数量关系,不用证明.
