浙江省历年（2018-2022年）真题分类汇编专题3 探索数...

更新时间：2022-08-22 浏览次数：87 类型：二轮复习

一、单选题

1. (2021·绍兴) 数学兴趣小组同学从“中国结”的图案（图1）中发现，用相同的菱形放置，可得到更多的菱形.如图2，用2个相同的菱形放置，得到3个菱形.下面说法正确的是（）

A . 用3个相同的菱形放置，最多能得到6个菱形 B . 用4个相同的菱形放置，最多能得到16个菱形 C . 用5个相同的菱形放置，最多能得到27个菱形 D . 用6个相同的菱形放置，最多能得到41个菱形

答案解析收藏纠错 + 选题
2. 某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品，将这些作品排成一个矩形(作品不完全重合)，现需要在每张作品的四个角落都钉上图钉，如果作品有角落相邻，那么相邻的角落共享一枚图钉(例如，用9枚图钉将4张作品钉在墙上，如图)，若有34枚图钉可供选用，则最多可以展示绘画作品（）

A . 16张 B . 18张 C . 20张 D . 21张

答案解析收藏纠错 + 选题
3. (2018·绍兴) 某班要在一面墙上同时展示数张形状、大小均相同的矩形绘画作品，将这些作品拍成一个矩形（作品不完全重合）。现需要在每张作品的四个角落都钉上图钉，如果作品有角落相邻，那么相邻的角落共享一枚图钉（例如，用9枚图钉将4张作品钉在墙上，如图）。若有34枚图钉可供选用，则最多可以展示绘画作品（）

A . 16张 B . 18张 C . 20张 D . 21张

答案解析收藏纠错 + 选题

二、填空题

4. (2024九上·宝山开学考) 定义一种新运算：对于任意的非零实数a，b，a $\text{[math]}$ b= $\text{[math]}$ ．若(x+1) $\text{[math]}$ x= $\text{[math]}$ ，则x的值为

答案解析收藏纠错 + 选题
5. (2021·嘉兴) 观察下列等式：1＝1²﹣0² ， 3＝2²﹣1² ， 5＝3²﹣2² ， …按此规律，则第n个等式为2n﹣1＝．

答案解析收藏纠错 + 选题
6. (2019·台州) 砸金蛋游戏：把210个“金蛋”连续编号为1，2，3，…，210，接着把编号是3的整数倍的“金蛋”全部砸碎，然后将剩下的”金蛋”重新连续编号为1，2，3，…，接着把编号是3的整数倍的“金蛋”全部砸碎…按照这样的方法操作，直到无编号是3的整数倍的“金蛋”为止。操作过程中砸碎编号是“66” “金蛋”共个

答案解析收藏纠错 + 选题
7. (2018·衢州) 定义；在平面直角坐标系中，一个图形先向右平移a个单位，再绕原点按顺时针方向旋转θ角度，这样的图形运动叫做图形的γ（a，θ）变换。
如图，等边△ABC的边长为1，点A在第一象限，点B与原点O重合，点C在x轴的正半轴上．△A₁B₁C₁就是△ABC经γ（1，180°）变换后所得的图形．
若△ABC经γ（1，180°）变换后得△A₁B₁C₁ ， △A₁B₁C₁经γ（2，180°）变换后得△A₂B₂C₂ ， △A₂B₂C₂经γ（3，180°）变换后得△A₃B₃C₃ ，依此类推……
△A_n-1B_n-1C_n-1经γ（n，180°）变换后得△A_nB_nC_n ，则点A₁的坐标是，点A₂₀₁₈的坐标是。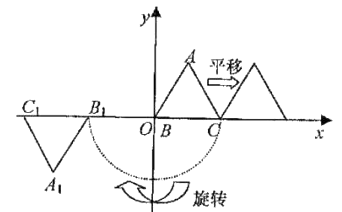

答案解析收藏纠错 + 选题

三、综合题

8. (2024九上·石家庄期末) 设 $\text{[math]}$ 是一个两位数，其中a是十位上的数字（1≤a≤9）．例如，当a＝4时， $\text{[math]}$ 表示的两位数是45．
1. （1）尝试：
  ①当a＝1时，15²＝225＝1×2×100＋25；
  
  ②当a＝2时，25²＝625＝2×3×100＋25；
  
  ③当a＝3时，35²＝1225＝；
  
  ……
2. （2）归纳： $\text{[math]}$ 与100a(a＋1)＋25有怎样的大小关系？试说明理由．
3. （3）运用：若 $\text{[math]}$ 与100a的差为2525，求a的值．
答案解析收藏纠错 + 选题
9. 观察下面的等式： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，……
1. （1）按上面的规律归纳出一个一般的结论(用含n的等式表示，n为正整数)．
2. （2）请运用分式的有关知识，推理说明这个结论是正确的。
答案解析收藏纠错 + 选题
10. (2019·衢州) 如图，由两个长为2，宽为1的长方形组成“7”字图形。
1. （1）将一个“7”字图形按如图摆放在平面直角坐标系中，记为“7”字图形ABCDEF，其中顶点A位于x轴上，顶点B，D位于y轴上，O为坐标原点，则 $\text{[math]}$ 的值为 .
2. （2）在（1）的基础上，继续摆放第二个“7”字图形得顶点F₁ ，摆放第三个“7”字图形得顶点F₂ ，依此类推，…，摆放第a个“7”字图形得顶点F_n-1 ， …，则顶点F₂₀₁₉的坐标为 .
答案解析收藏纠错 + 选题
11. (2019·衢州) 定义：在平面直角坐标系中，对于任意两点A（a，b），B(c，d)，若点T（x，y)满足x= $\text{[math]}$ ，y= $\text{[math]}$ ，那么称点T是点A，B的融合点。
例如：A（-1，8），B（4，-2），当点T（x，y）满是x= $\text{[math]}$ =1，y= $\text{[math]}$ =2时，则点T（1，2）是点A，B的融合点，
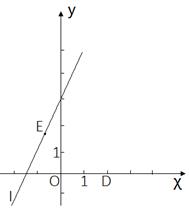
1. （1）已知点A（-1，5），B(7，7)，C（2，4），请说明其中一个点是另外两个点的融合点。
2. （2）如图，点D（3，0），点E（t，2t+3）是直线l上任意一点，点T（x，y)是点D，E的融合点。
  ①试确定y与x的关系式。
  
  ②若直线ET交x轴于点H，当△DTH为直角三角形时，求点E的坐标。
答案解析收藏纠错 + 选题