浙江省历年（2018-2022年）真题分类汇编专题36 圆的...

更新时间：2022-10-11 浏览次数：82 类型：二轮复习

一、单选题

1. (2021·天河模拟) 尺规作图特有的魅力曾使无数人沉湎其中．传说拿破仑通过下列尺规作图考他的大臣：
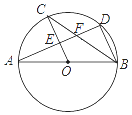
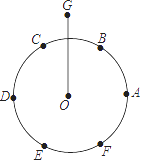
①将半径为r的⊙O六等分，依次得到A，B，C，D，E，F六个分点；②分别以点A，D为圆心，AC长为半径画弧，G是两弧的一个交点；③连结OG．问：OG的长是多少？大臣给出的正确答案应是（）

A . $\text{[math]}$ r B . （1+ $\text{[math]}$ ）r C . （1+ $\text{[math]}$ ）r D . $\text{[math]}$ r

答案解析收藏纠错 + 选题
2. 用反证法证明时，假设结论“点在圆外”不成立，那么点与圆的位置关系只能是（）

A . 点在圆内 B . 点在圆上 C . 点在圆心上 D . 点在圆上或圆内

答案解析收藏纠错 + 选题
3. (2019九上·绵阳期中) 如图，AC是⊙O的直径，弦BD⊥AO于E，连接BC，过点O作OF⊥BC于F，若BD=8cm，AE=2cm，则OF的长度是（）

A . 3cm B . $\text{[math]}$ cm C . 2.5cm D . $\text{[math]}$ cm

答案解析收藏纠错 + 选题
4. (2018·衢州) 如图，点A，B，C在⊙O上，∠ACB=35°，则∠AOB的度数是（）

A . 75° B . 70° C . 65° D . 35°

答案解析收藏纠错 + 选题
5. (2021九上·路北期中) 一块圆形宣传标志牌如图所示，点A，B，C在⊙O上，CD垂直平分AB于点D，现测得AB=8dm，DC=2dm，则圆形标志牌的半径为（）

A . 6dm B . 5dm C . 4dm D . 3dm

答案解析收藏纠错 + 选题
6. (2020·绍兴) 如图，点A，B，C，D，E均在⊙O上，∠BAC=15°，∠CED=30°，则∠BOD的度数为（）

A . 45° B . 60° C . 75° D . 90°

答案解析收藏纠错 + 选题
7. (2020·湖州) 如图，已知四边形ABCD内接于⊙O，∠ABC＝70°，则∠ADC的度数是（）

A . 70° B . 110° C . 130° D . 140°

答案解析收藏纠错 + 选题
8. (2020·嘉兴·舟山) 如图，在等腰△ABC中， AB=AC=2 $\text{[math]}$ ，BC=8，按下列步骤作图：

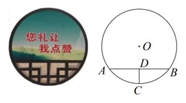
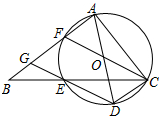
①以点A为圆心，适当的长度为半径作弧，分别交AB，AC于点E，F，再分别以点E，F为圆心，大于 $\text{[math]}$ EF的长为半径作弧相交于点H，作射线AH；②分别以点A，B为圆心，大于 $\text{[math]}$ AB的长为半径作弧相交于点M，N，作直线MN，交射线AH于点0；③以点为圆心，线段OA长为半径作圆。则⊙O的半径为（）

A . 2 $\text{[math]}$ B . 10 C . 4 D . 5

答案解析收藏纠错 + 选题
9. (2020·杭州) 如图，已知BC是⊙O的直径，半径OA⊥BC，点D在劣弧AC上(不与点A，点C重合)，BD与OA交于点E，设∠AED=α，∠AOD=β，则（）

A . 3α+β=180° B . 2α+β=180° C . 3α-β=90° D . 2α-β=90°

答案解析收藏纠错 + 选题

二、填空题

10. (2018·杭州) 如图，AB是⊙的直径，点C是半径OA的中点，过点C作DE⊥AB，交O于点D，E两点，过点D作直径DF，连结AF，则∠DEA=。

答案解析收藏纠错 + 选题
11. 如图，在⊙O中，弦 $\text{[math]}$ ，点C在AB上移动，连结OC，过点C作CD⊥OC交⊙O于点D，则CD的最大值为．

答案解析收藏纠错 + 选题
12. (2019九上·石嘴山期中) 已知一条弧所对的圆周角的度数是15°，则它所对的圆心角的度数是.

答案解析收藏纠错 + 选题
13. (2020·湖州) 如图，已知AB是半圆O的直径，弦CD∥AB，CD＝8，AB＝10，则CD与AB之间的距离是.

答案解析收藏纠错 + 选题

三、综合题

14. (2022九上·余杭期中) 如图，已知AB是⊙O的直径，C，D是⊙O上的点，OC∥BD，交AD于点E，连结BC．
1. （1）求证：AE=ED；
2. （2）若AB=10，∠CBD=36°，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
15. (2021·夏津模拟) 如图，△ABC内接于⊙O，AB为⊙O的直径，AB=10，AC=6。连结OC，弦AD分别交OC，BC于点E，F，其中点E是AD的中点。
1. （1）求证：∠CAD=∠CBA。
2. （2）求OE的长。
答案解析收藏纠错 + 选题
16. (2020·温州) 如图，C，D为⊙O上两点，且在直径AB两侧，连结CD交AB于点E，G是 $\text{[math]}$ 上一点，∠ADC=∠G。
1. （1）求证：∠1=∠2。
2. （2）点C关于DG的对称点为F，连结CF.当点F落在直径AB上时，CF=10，tan∠1= $\text{[math]}$ ，求⊙O的半径。
答案解析收藏纠错 + 选题
17. (2020·五峰模拟) 如图，在△ABC中，∠BAC＝90°，点E在BC边上，且CA＝CE，过A，C，E三点的⊙O交AB于另一点F，作直径AD，连结DE并延长交AB于点G，连结CD，CF．
1. （1）求证：四边形DCFG是平行四边形；
2. （2）当BE＝4，CD＝ $\text{[math]}$ AB时，求⊙O的直径长．
答案解析收藏纠错 + 选题
18. (2019·杭州) 如图，已知锐角三角形ABC内接于⊙O，OD⊥BC于点D，连接OA.
1. （1）若∠BAC=60°，
  ①求证：OD= $\text{[math]}$ OA.
  ②当OA=1时，求△ABC面积的最大值。
2. （2）点E在线段OA上，（OE=OD.连接DE，设∠ABC=m∠OED.∠ACB=n∠OED（m，n是正数）.若∠ABC<∠ACB，求证：m-n+2=0.
答案解析收藏纠错 + 选题