2022-2023学年冀教版数学九年级上册23.3方差同步...

更新时间：2022-08-17 浏览次数：34 类型：同步测试

一、单选题

1. 我校准备挑选一名跳高运动员参加全市中学生运动会，对跳高运动队的甲、乙两名运动员进行了8次选拔比赛.他们的成绩（单位：m）如下：
甲
1.70
1.65
1.68
1.69
1.72
1.73
1.68
1.67
乙
1.60
1.73
1.72
1.61
1.62
1.71
1.70
1.75
借助计算器判断运动员的成绩更为稳定的是（）

A . 甲 B . 乙 C . 一样稳定 D . 无法判断

答案解析收藏纠错 + 选题
2. (2023九上·盐城期末) 小明根据演讲比赛中9位评委所给的分数制作了如下表格：

平均数

中位数

众数

方差

8.0

8.2

8.3

0.2

如果去掉一个最高分和一个最低分，那么表格中数据一定不发生变化的是（）

A . 平均数 B . 中位数 C . 众数 D . 方差

答案解析收藏纠错 + 选题

3. (2022八下·遂昌期中) 为迎接建党一百周年，某班50名同学进行了党史知识竞赛，测试成绩统计如下表，其中有两个数据被遮盖.下列关于成绩的统计量中，与被遮盖的数据无关的是（）

成绩/分	91	92	93	94	95	96	97	98	99	100
人数	■	■	1	2	3	5	6	8	10	12

A . 平均数，方差 B . 中位数，方差 C . 中位数，众数 D . 平均数，众数

答案解析收藏纠错 + 选题

4. (2021九上·信都月考) 已知一组数据的方差s²＝ $\text{[math]}$ [（6﹣7）²+（10﹣7）²+（a﹣7）²+（b﹣7）²+（8﹣7）²]（a，b为常数），则a+b的值为（）

A . 5 B . 7 C . 10 D . 11

答案解析收藏纠错 + 选题
5. (2023八下·安庆期末) 某选手在比赛中的成绩（单位：分）分别是90，87，92，88，93，方差是5.2（单位：分²），如果去掉一个最高分和一个最低分，那么该选手成绩的方差会（）

A . 变大 B . 不变 C . 变小 D . 不确定

答案解析收藏纠错 + 选题
6. (2021八上·梅县区期末) 在第60届国际数学奥林匹克比赛中，中国队荣获团体总分第一名.我国参赛选手比赛成绩的方差计算公式为： $\text{[math]}$ ，下列说法错误的是（）.

A . 我国一共派出了6名选手 B . 我国参赛选手的平均成绩为38分 C . 我国选手比赛成绩的中位数为38 D . 我国选手比赛成绩的团体总分为228分

答案解析收藏纠错 + 选题
7. 用计算器计算方差时，要首先进入统计计算状态，需要按键（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. 用科学计算器求得271，315，263，289，300，277，286，293，297，280的平均数与方差（精确到0.1）分别为（）.

A . 287.1，14.4 B . 287，14 C . 287，14.4 D . 14.4，287.1

答案解析收藏纠错 + 选题
9. (2022八下·乐清期末) 老师对甲、乙两位同学近六次数学测试成绩进行统计分析，已知甲的方差是2.2，甲的成绩比乙的成绩更稳定，则乙的方差可能是（）

A . 1.8 B . 2 C . 2.2 D . 3.2

答案解析收藏纠错 + 选题
10. (2022八下·新昌期末) 2021 年，党中央国务院赋予浙江省建设“共同富裕示范区”的光荣使命，共同富裕的要求是：在消除两极分化和贫穷基础上实现普遍富裕．下列有关人均收入的统计量特征中，最能体现共同富裕要求的是（）

A . 平均数大，方差大 B . 平均数大，方差小 C . 平均数小，方差小 D . 平均数小，方差大

答案解析收藏纠错 + 选题

二、填空题（每空2分，共10分）

11. (2022八下·五华期末) 农科院助农团队在某地各选6块试验田试种甲、乙两种杂交水稻，收获后统计结果为： $\text{[math]}$ 千克/亩， $\text{[math]}$ ， $\text{[math]}$ 千克/亩， $\text{[math]}$ ，则品种更适合在该地区推广．（填“甲”或“乙”）

答案解析收藏纠错 + 选题

12. (2021九上·本溪期末) 某校射击队从甲、乙、丙、丁四人中选拔一人参加射击比赛，在选拔赛中每人射击10次，计算他们10发成绩的平均数（环）及方差如下表.

	甲	乙	丙	丁
平均数	8.2	8.0	8.2	8.0
方差	2.0	1.8	1.5	1.6

请你根据表中数据选择其中一人参加比赛，最合适的人选是.

答案解析收藏纠错 + 选题

13. (2022八下·德阳期末) 某班有50人，一次数学测试后，老师对测试成绩进行了统计．由于小明没有参加此次集体测试，因此计算其他49人的平均分为92分，方差 $\text{[math]}$ ．后来小明进行了补测，成绩是92分，则该班50人的数学测试成绩的方差 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2022八下·大兴期末) 现有5名同学的身高分别为165，172，168，170，175（单位：厘米）．增加1名身高为170的同学后，这6名同学身高的平均数和方差与原来相比，平均数（填“变大”、“变小”“不变”），方差（填“变大”、“变小”、“不变”）．

答案解析收藏纠错 + 选题

三、综合题（共5题，共60分）

15. (2021九上·扬州月考) 甲、乙两人在相同的情况下各打靶6次，每次打靶的成绩依次如下（单位：环）：
甲：10，7，8，7，8，8
乙：5，6，10，8，9，10
1. （1）甲成绩的众数，乙成绩的中位数.
2. （2）计算乙成绩的平均数和方差；
3. （3）已知甲成绩的方差是1环，则的射击成绩离散程度较小.（填“甲”或“乙”）
答案解析收藏纠错 + 选题

16. (2021九上·邗江期末) 某中学九年级学生开展踢毽子活动，每班派5名学生参加，按团体总分排列名次，在规定时间内每人踢100个以上（含100）为优秀.下表是成绩最好的甲班和乙班5名学生的比赛成绩（单位：个）

	1号	2号	3号	4号	5号	总数
甲班	100	98	110	89	103	500
乙班	90	97	101	113	99	500

经统计发现两班5名学生踢毽子的总个数相等，此时有学生建议，可以通过考查数据中的其他信息为参考，请你回答下列问题：

（1）甲班比赛数据的中位数为，乙班比赛数据的平均数为；
（2）计算两班比赛数据的方差；
（3）根据以上信息，你认为应该把冠军奖状发给哪一个班？简述理由.

答案解析收藏纠错 + 选题

17. (2021九上·江油开学考) 某中学举行“中国梦•校园好声音”歌手大赛，高、初中部根据初赛成绩，各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出5名选手的决赛成绩如图所示.
1. （1）根据图示填表：
  
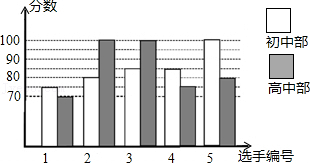
  平均数（分）
  
  中位数（分）
  
  众数（分）
  
  初中部
  
  85
  
  高中部
  
  85
  
  100
2. （2）结合两队成绩的平均数和中位数，分析哪个队的决赛成绩较好；
3. （3）计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
答案解析收藏纠错 + 选题

18. (2020九上·高淳期中) 甲、乙两位同学5次数学选拔赛的成绩统计如表，他们5次考试的总成绩相同，请同学们完成下列问题：

	第1次	第2次	第3次	第4次	第5次
甲成绩	80	40	70	50	60
乙成绩	70	50	70	a	70

（1）统计表中，a＝，甲同学成绩的极差为；
（2）小颖计算了甲同学的成绩平均数为60，方差是S_甲²＝ $\text{[math]}$ [（80﹣60）²+（40﹣60）²+（70﹣60）²+（50﹣60）²+（60﹣60）²]＝200.请你求出乙同学成绩的平均数和方差；
（3）从平均数和方差的角度分析，甲、乙两位同学谁的成绩更稳定.

答案解析收藏纠错 + 选题

19. (2020九上·滦州期中) 嘉淇同学利用业余时间进行射击训练，一共射击7次，经过统计，制成如图12所示的折线统计图．
1. （1）这组成绩的众数是；
2. （2）求这组成绩的方差；
3. （3）若嘉淇再射击一次（成绩为整数环），得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数，求第8次的射击成绩的最大环数．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中