湖北省武汉市江夏区华一寄宿学校2022-2023学年九年级上...

更新时间：2022-10-27 浏览次数：83 类型：月考试卷

一、选择题（每小题3分，共30分）

1. (2022九上·岳麓月考) 把方程2x＝x²﹣3化为一般形式，若二次项系数为1，则一次项系数及常数项分别为（）

A . 2、3 B . ﹣2、3 C . 2、﹣3 D . ﹣2、﹣3

答案解析收藏纠错 + 选题
2. (2022九上·岳麓月考) 下列图形中，既是轴对称图形又是中心对称图形的是（）

A . 三角形 B . 等边三角形 C . 平行四边形 D . 菱形

答案解析收藏纠错 + 选题
3. (2022九上·岳麓月考) 将抛物线y＝ $\text{[math]}$ （x+1）²﹣1平移后得到抛物线y＝ $\text{[math]}$ x² ．下列平移方法正确的是（）

A . 先向右平移1个单位，再向上平移1个单位 B . 先向左平移1个单位，再向下平移1个单位 C . 先向左平移1个单位，再向上平移1个单位 D . 先向右平移1个单位，再向下平移1个单位

答案解析收藏纠错 + 选题
4. (2022九上·岳麓月考) 如图，在△ABC中，∠B＝55°，∠ACB＝30°，将△ABC绕点C顺时针旋转n度（0＜n＜180）得到△EDC，若CE∥AB，则n的值为（　　）

A . 65 B . 90 C . 95 D . 125

答案解析收藏纠错 + 选题
5. (2022九上·岳麓月考) 用配方法解方程x²﹣4x﹣3＝0．下列变形正确的是（）

A . （x﹣4）²＝19 B . （x﹣2）²＝7 C . （x﹣2）²＝1 D . （x+2）²＝7

答案解析收藏纠错 + 选题
6. (2022九上·岳麓月考) 在同一平面直角坐标系中，一次函数y＝kx﹣1与二次函数y＝kx²＋3的大致图象可以是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2022九上·岳麓月考) 已知关于x的一元二次方程x²﹣mnx+m+n＝0，其中m，n在数轴上的对应点如图所示，则这个方程的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 无法确定

答案解析收藏纠错 + 选题
8. (2022九上·岳麓月考) 如图所示，在菱形ABCD中，AB＝6，∠BAD＝120°，△AEF为正三角形，点E、F分别在菱形的边BC、CD上滑动，且E、F不与B、C、D重合．当点E、F在BC、CD上滑动时，△CEF的面积最大值是（）

A . 4 $\text{[math]}$ B . $\text{[math]}$ C . 3 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022九上·岳麓月考) 如图，在平面直角坐标系中，已知A（10，0），点P为线段OA上任意一点．在直线y＝ $\text{[math]}$ x上取点E，使PO＝PE，延长PE到点F，使PA＝PF，分别取OE、AF中点M、N，连接MN，则MN的最小值是（）

A . 4.8 B . 5 C . 5.4 D . 6

答案解析收藏纠错 + 选题
10. (2022九上·岳麓月考) 对于一个函数，自变量x取a时，函数值y也等于a，我们称a为这个函数的不动点．如果二次函数y＝x²+2x+c有两个相异的不动点x₁ ， x₂ ，且x₁＜2＜x₂ ，则c的取值范围是（）

A . c＜﹣3 B . c＜﹣8 C . c＜﹣6 D . c＜﹣1

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共18分）

11. (2023九上·莎车月考) 一元二次方程x²+3x=0的解是．

答案解析收藏纠错 + 选题
12. (2022九上·岳麓月考) 关于x的一元二次方程kx²+2x﹣1=0有两个不相等的实数根，则k的取值范围是．

答案解析收藏纠错 + 选题
13. (2022九上·岳麓月考) 设a、b为x²+x﹣2021＝0的两个实数根，则a³+a²+3a+2024b＝．

答案解析收藏纠错 + 选题
14. (2024九上·平凉期中) 圣诞节时，某班一个小组有x人，他们每两人之间互送贺卡一张，已知全组共送贺卡110张，则可列方程为．

答案解析收藏纠错 + 选题
15. (2023九上·怀仁月考) 如图，已知A（1，1），B（3，9）是抛物线y＝x²上的两点，在y轴上有一动点P，当△PAB的周长最小时，则此时△PAB的面积为．

答案解析收藏纠错 + 选题
16. (2022九上·岳麓月考) 下列关于二次函数y＝x²﹣2mx+m²﹣1的结论：
①该函数图象的对称轴为直线x＝m；
②若函数图象的顶点为M，与x轴交于A、B两点，则S_△_ABM为定值；
③若P（x₁ ， y₁），Q（x₂ ， y₂）两点在该函数图象上，且x₁＞x₂ ， x₁+x₂＞2m，则有y₁＜y₂；
④该函数图象与y轴交于C点，与x轴交于A、B两点，△ABC不可能为直角三角形．
其中正确的结论是．

答案解析收藏纠错 + 选题

三、解答题（共72分）

17. (2022九上·岳麓月考) 用公式法解下列方程：2x²﹣3x+1＝0．

答案解析收藏纠错 + 选题
18. (2023九上·仁寿月考) 已知关于x的方程x²+（2k﹣1）x+k²﹣1=0有两个实数根x₁ ， x₂ ．
1. （1）求实数k的取值范围；
2. （2）若x₁ ， x₂满足x₁²+x₂²=16+x₁x₂ ，求实数k的值．
答案解析收藏纠错 + 选题
19. (2022九上·岳麓月考) .已知抛物线y＝x²+bx+c的对称轴为x＝2，且过点C（0，3）
1. （1）求此抛物线的解析式；
2. （2）证明：该抛物线恒在直线y＝﹣2x+1上方．
答案解析收藏纠错 + 选题
20. (2022九上·岳麓月考) 如图，Rt△ABC中，∠C＝90°，BC＝a，AC＝b（a＜b），AB＝5，a，b是方程x²﹣（m﹣1）x+（m+4）＝0的两根
1. （1）求a，b；
2. （2） P，Q两点分别从A，C出发，分别以每秒2个单位，1个单位的速度沿边AC，BC向终点C，B运动，（有一个点达到终点则停止运动），求经过多长时间后PQ＝2？
答案解析收藏纠错 + 选题
21. (2022九上·岳麓月考) 如图，由边长为1的小正方形构成的网格中，每个小正方形的顶点叫做格点，△ABC的顶点在格点上．请用无刻度尺按要求作图：
1. （1）作△ABC的高AH；
2. （2） ①找一格点D使AD⊥AC且AD＝AC；
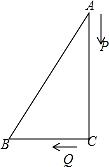
  ②连接CD，在CD上画出一点F，连AF，使AF将四边形ABCD的面积平分．
答案解析收藏纠错 + 选题
22. (2022九上·岳麓月考) 如图，用长30米的竹篱笆围成一个矩形菜园，其中一面靠墙，墙长10米，墙的对面有一个2米宽的门，设垂直于墙的一边长为x米，菜园的面积为S平方米．
1. （1）直接写出S与x的函数关系式；
2. （2）若菜园的面积为96平方米，求x的值；
3. （3）若在墙的对面再开一个宽为a（0＜a＜3）米的门，且面积S的最大值为124平方米，直接写出a的值．
答案解析收藏纠错 + 选题
23. (2022九上·岳麓月考) 在△ABE和△CDE中，∠ABE＝∠DCE＝90°，AB＝BE，CD＝CE．
1. （1）连接AD、BC，点M、N分别为AD、BC的中点，连接MN，
  ①如图1，当B、E、C三点在一条直线上时，MN与BC关系是 ▲ ．
  ②如图2，当等腰Rt△CDE绕点E顺时针旋转时，①中的结论还成立吗？如果成立，请证明你的结论；如果不成立，请说明理由．
2. （2）如图3，当等腰Rt△CDE绕点E顺时针旋转时，连接AC、BD，点P、Q分别为BD、AC的中点，连接PQ，若AB＝13，CD＝5，则PQ的最大值是，此时以A、B、C、D为顶点的四边形的面积为．
答案解析收藏纠错 + 选题
24. (2022九上·岳麓月考) 如图，平面直角坐标系中，直线y＝x+4分别交x、y轴于A、B两点，点P为线段AB的中点．
1. （1）直接写出点P的坐标；
2. （2）如图1，点C是x轴正半轴上的一动点，过点P作PD⊥PC交y轴正半轴于点D，连接CD，点M、N分别是CD、OB的中点，连接MN，求∠MNO的度数；
3. （3）如图2，点Q是x轴上的一个动点，连接PQ．把线段PQ绕点Q逆时针旋转90°至线段QT，连接PT、OT．当PT+OT的值最小时，求此时点T的坐标．
答案解析收藏纠错 + 选题