一、选择题(本大题10小题,每小题3分,共30分)
-
-
A . 1,2,4
B . 4,5,9
C . 4,6,9
D . 5,5,11
-
A . 三角形具有稳定性
B . 三角形内角和等于180°
C . 两点之间线段最短
D . 同位角相等,两直线平行拉杆
-
4.
(2022八上·龙湖期中)
如图,在△ABC和△DEF中,AB=DE,∠A=∠D,添加一个条件不能判定这两个三角形全等的是( )

A . AC=DF
B . ∠B=∠E
C . BC=EF
D . ∠C=∠F
-
-
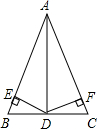
A . ∠B=∠C
B . BD=CD
C . AB=2BD
D . AD平分∠BAC
-
A . 20°
B . 30°
C . 50°
D . 70°
-
A . 5
B . 4
C . 8
D . 4或8
-
9.
(2022八上·龙湖期中)
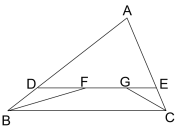
如图,DE=11,FG=3,BF、CG分别平分∠ABC、∠ACB,DE∥BC.
则BD+CE=( )
A . 3
B . 11
C . 7
D . 8
-
10.
(2022八上·龙湖期中)
如图,在平面直角坐标系xOy中,已知点A的坐标是(0,2),以OA为边在右侧作等边三角形OAA
1 , 过点A
1作x轴的垂线,垂足为点O
1 , 以O
1A
1为边在右侧作等边三角形O
1A
1A
2 , 再过点A
2作x轴的垂线,垂足为点O
2 , 以O
2A
2为边在右侧作等边三角形O
2A
2A
3 , …,按此规律继续作下去,得到等边三角形O
2022A
2022A
2023 , 则点A
2023的纵坐标为( )

A . ( )2021
B . (
)2021
B . ( )2022
C . (
)2022
C . ( )2023
D . (
)2023
D . ( )2024
)2024
二、填空题(本大题5小题,每小题3分,共15分)
-
-
-
-
14.
(2022八上·龙湖期中)
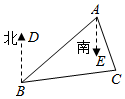
如图,是A、B、C三个村庄的平面图,已知B村在A村的南偏西50°方向,C村在A村的南偏东15°方向,C村在B村的北偏东85°方向,则从C村观测A、B两村的视角∠ACB的度数为
。
-
15.
(2022八上·龙湖期中)
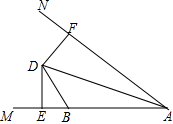
如图,D是∠MAN角平分线上一点,点B是射线AM上一点,DE⊥AM于点E,DF⊥AN于点F,连接AD.在射线AN上取一点C,使得DC=DB,若AB=7,BE=2,则AC的长为
。
三、解答题(一)(本大题3小题,每小题8分,共24分)
-
-
-
(2)
若∠A=40°,∠D=80°,则∠E=(直接写结果)
-
-
-
(2)
若∠BAC=78°,则∠C的度数为(直接写结果)
-
-
(1)
作图:作AB边的垂直平分线分别交AB,AC于点E,F.(用尺规作图,保留作图痕迹,不要求写作法);
-
(2)
在(1)的条件下,连接BF,则△FBC的周长为(直接写结果)
四、解答题(二)(本大题3小题,每小题9分,共27分)
-
19.
(2022八上·龙湖期中)
如图,在△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=56°,∠C=70°.

-
-
-
-
-
(2)
若AB=8,S△ABC=36,求DE的长.
-
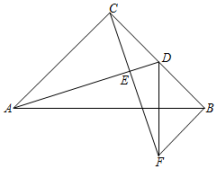
21.
(2022八上·龙湖期中)
如图,在Rt△ABC中,∠ACB=90°,AC=BC,D为BC的中点,CE⊥AD,垂足为点E,BF∥AC,交CE的延长线于点F.
-
-
五、解答题(三)(本大题2小题,每小题12分,共24分)
-
22.
(2022八上·龙湖期中)
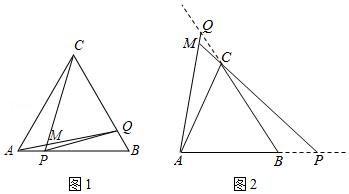
如图,点P、Q分别是等边△ABC边AB、BC上的动点(不与端点重合),点P、点Q以相同的速度,同时从点A、点B出发.
-
(1)
如图1,连接AQ、CP.求证:△ABQ≌△CAP;
-
(2)
如图1,当点P、Q分别在AB、BC边上运动时,AQ、CP相交于点M,∠QMC的大小是否变化?若变化,请说明理由;若不变,求出它的度数;
-
(3)
如图2,当点P、Q运动到AB、BC的延长线上时,直线AQ、CP相交于M,∠QMC的大小是否变化?若变化,请说明理由;若不变,请直接写出∠QMC的度数.
-
-
(1)
【模型呈现】
如图1,∠BAD=90°,AB=AD,过点B作BC⊥AC于点C,过点D作DE⊥AC于点E.由∠1+∠2=∠2+∠D=90°,得∠1=∠D.又∠ACB=∠AED=90°,可以推理得到△ABC≌△DAE.进而得到AC=,BC=.我们把这个数学模型称为“K字”模型或“一线三等角”模型;
-
(2)
【模型应用】
如图2,∠BAD=∠CAE=90°,AB=AD,AC=AE,连接BC,DE,且BC⊥AF于点F,DE与直线AF交于点G.求证:点G是DE的中点;
-
(3)
如图3,在平面直角坐标系xOy中,点A的坐标为(2,6),点B为平面内任一点.若△AOB是以OA为斜边的等腰直角三角形,请直接写出点B的坐标.
 B .
B .  C .
C .  D .
D .