 B .
B .  C .
C .  D .
D . 
① 以点O 为圆心,适当长为半径画弧,交OA于点M , 交OB 于点N;② 分别以点M , N为圆心,大于 MN 的长为半径画弧,两弧在∠AOB 内部交于点C;③ 画射线OC , OC即为所求.根据上面的作法,可得△OMC≌△ONC , 其判定的依据是( )



 B .
B .  C .
C .  D .
D . 



我们定义:如果两个实数的差等于这两个实数的商,那么这两个实数就叫做“差商等数对”.即:如果 , 那么α与b就叫做“差商等数对”,记为
. 例如:
;
;则称数对
,
是“差商等数对”.
根据上述材料,解决下列问题:
①②
③
20 | 40 | 60 | … | |
… |
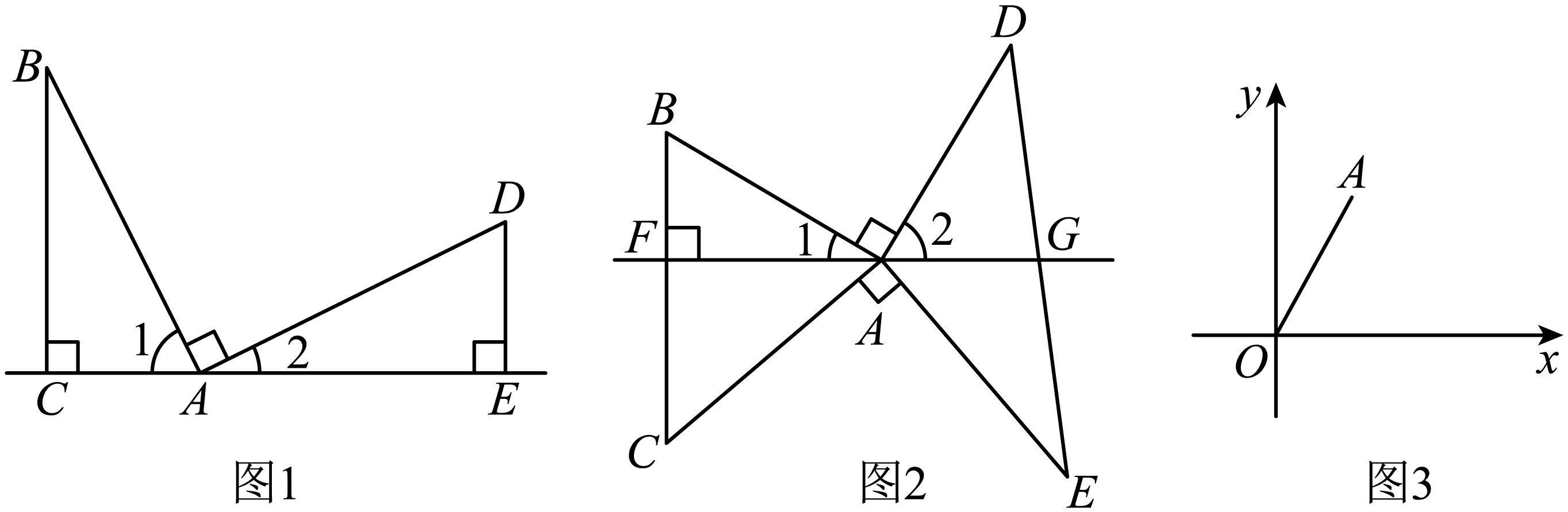
如图1, , 过点B作
于点C,过点D作
于点E.由
, 得
. 又
, 可以推理得到
. 进而得到AC=,BC=.我们把这个数学模型称为“K字”模型或“一线三等角”模型;
①如图2, , 连接
, 且
于点F,
与直线
交于点G.求证:点G是
的中点;
②如图3,在平面直角坐标系xOy中,点A的坐标为 , 点B为平面内任一点.若
是以
为斜边的等腰直角三角形,请直接写出点B的坐标.