河南省周口市扶沟县大李庄乡初级中学2022-2023学年九年...

更新时间：2024-07-13 浏览次数：72 类型：期末考试

一、单选题

1. (2024九上·长春月考) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 都是锐角， $\text{[math]}$ ， $\text{[math]}$ ，则对 $\text{[math]}$ 的形状最确切的判断是（）

A . 锐角三角形 B . 等腰直角三角形 C . 等腰三角形 D . 直角三角形

答案解析收藏纠错 + 选题
2. (2023九上·扶沟期末) 如图是某圆锥的主视图和左视图，该圆锥的侧面积是（）

A . 15π B . 16π C . 20π D . 25π

答案解析收藏纠错 + 选题
3. (2023九上·扶沟期末) 如图， $\text{[math]}$ 经过位似变换得到 $\text{[math]}$ ，点O是位似中心且 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 的面积比是（）

A . 2：1 B . 3：1 C . 4：1 D . 6：1

答案解析收藏纠错 + 选题
4. (2023八下·东阳月考) 如图，某广场有一块圆形的花圃，中间有一个正方形的水池，测量出除水池外圆内可种植面积是120m² ，从水池边到圆周，每边都相距4m，设正方形的边长为xm，则可列出的方程是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023九上·扶沟期末) 如图，某加油站计划在地下修建一个容积为 $\text{[math]}$ 的圆柱形石油储存室，则储存室的底面积S（单位： $\text{[math]}$ ）与其深度h（单位：m）的函数图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
6. (2023九下·冷水滩期中) 将关于x的一元二次方程 $\text{[math]}$ 变形为 $\text{[math]}$ ，就可以将 $\text{[math]}$ 表示为关于x的一次多项式，从而达到“降次”的目的，又如 $\text{[math]}$ …，我们将这种方法称为“降次法”，通过这种方法可以化简次数较高的代数式.根据“降次法”，已知： $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023九上·扶沟期末) 在小明住的小区有一条笔直的路，路中间有一盏路灯，一天晚上他行走在这条路上如图，当他从A点走到B点的过程，他在灯光照射下的影长l与所走路程s的变化关系图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2023九上·扶沟期末) 定义：给定关于x的函数y，对于该函数图象上的任意两点 $\text{[math]}$ ，当 $\text{[math]}$ 时，都有 $\text{[math]}$ ，称该函数为偶函数.根据以上定义，判断下面所给的函数为偶函数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023九上·扶沟期末) 如图， $\text{[math]}$ 是⊙O的直径，弦 $\text{[math]}$ ， $\text{[math]}$ ，若动点M以 $\text{[math]}$ 的速度从C点出发沿着C到A的方向运动，点N以 $\text{[math]}$ 的速度从A点出发沿着A到B的方向运动，当点M到达点A时，点N也随之停止运动，设运动时间为 $\text{[math]}$ ，当 $\text{[math]}$ 是直角三角形时，t的值为（）

A . $\text{[math]}$ B . 5s C . $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023九上·扶沟期末) 如图，在 $\text{[math]}$ 轴正半轴上依次截取 $\text{[math]}$ ，过点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、…… $\text{[math]}$ 分别作 $\text{[math]}$ 轴的垂线，与反比例函数 $\text{[math]}$ 交于点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、…、 $\text{[math]}$ ，连接 $\text{[math]}$ 、 $\text{[math]}$ 、… $\text{[math]}$ ，过点 $\text{[math]}$ 、 $\text{[math]}$ 、…、 $\text{[math]}$ 分别向 $\text{[math]}$ 、 $\text{[math]}$ 、…、 $\text{[math]}$ 作垂线段，构成的一系列直角三角形（图中阴影部分）的面积和等于（）.

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2023九上·扶沟期末) 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 绕点A旋转后能与 $\text{[math]}$ 重合，那么 $\text{[math]}$ 与 $\text{[math]}$ 的周长之比是.

答案解析收藏纠错 + 选题
12. (2023九上·扶沟期末) 已知点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线 $\text{[math]}$ 的图象上，判断 $\text{[math]}$ $\text{[math]}$ .

答案解析收藏纠错 + 选题
13. (2024九上·中山期中) 已知二次函数 $\text{[math]}$ 的图象和x轴有交点，则m的取值范围是.

答案解析收藏纠错 + 选题
14. (2023九上·扶沟期末) 如图，测得某医院的自动扶梯的长为m，自动扶梯与地面所成的角为α，则该自动扶梯到达的高度n为.

答案解析收藏纠错 + 选题
15. (2023九上·扶沟期末) 若二次函数 $\text{[math]}$ 的二次项系数比一次项系数小12，一次项系数比常数项大8，则这个二次函数的解析式为.

答案解析收藏纠错 + 选题

三、解答题

16. (2023九上·扶沟期末)
1. （1）解方程： $\text{[math]}$ ；
2. （2） $\text{[math]}$ .
答案解析收藏纠错 + 选题
17. (2023九上·扶沟期末) 某市政府为落实“保障性住房政策”，2018年已投入3亿元资金用于保障性住房建设，并规划投入资金逐年增加，到2020年底，将累计投入13.5亿元资金用于保障性住房建设.
1. （1）求到2020年底，这两年中投入资金的年平均增长率.（只列方程）
2. （2）设（1）中方程的两根分别为 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ 的值为18，求m的值.
答案解析收藏纠错 + 选题
18. (2023九上·扶沟期末) 如图，双曲线 $\text{[math]}$ 上的一点 $\text{[math]}$ ，其中 $\text{[math]}$ ，过点M作 $\text{[math]}$ 轴于点N，连接 $\text{[math]}$ .
1. （1）已知 $\text{[math]}$ 的面积是4，求k的值；
2. （2）将 $\text{[math]}$ 绕点M逆时针旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，且点O的对应点Q恰好落在该双曲线上，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
19. (2023九上·扶沟期末) 一个不透明的袋子中装有四个小球，上面分别标有数字 $\text{[math]}$ ， 0，1，2，它们除了数字不同外，其他完全相同.
1. （1）随机从袋子中摸出一个小球，摸出的小球上面标的数字为负数的概率是；
2. （2）彤彤先从袋子随机摸出一个小球，记下数字作为平面直角坐标系内点P的横坐标，然后放回搅匀，接着珊珊从袋子随机摸出一个小球，记下数字作为平面直角坐标系内点的纵坐标，如图，已知四边形 $\text{[math]}$ 的四个顶点的坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，请用列表法求点P落在四边形 $\text{[math]}$ 内（含边界）的概率.
答案解析收藏纠错 + 选题
20. (2023九上·扶沟期末) 如图， $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点O在 $\text{[math]}$ 上，以O为圆心， $\text{[math]}$ 为半径画⊙O，分别与边 $\text{[math]}$ 相交于点 $\text{[math]}$ ，垂足分别为E、D.
1. （1）求证： $\text{[math]}$ 是⊙O的切线；
2. （2）设 $\text{[math]}$ ，求 $\text{[math]}$ 的长（用含m的代数式表示）.
答案解析收藏纠错 + 选题
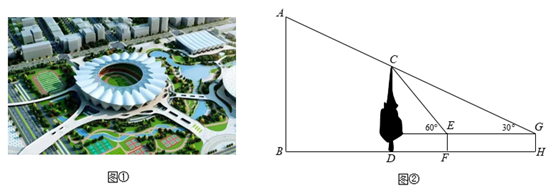
21. (2023九上·扶沟期末) 如图①，西安奥体中心体育场作为2021年第十四届全运会的主会场，以西安市花“石榴花”为构思，以“丝路起航，盛世之花”为立意，让建筑、自然与人共生共融.小明和数学实践小组的同学想知道西安奥体中心主体育场馆的高度，于是他们拿着测倾器和皮尺来到奥体中心，如图②所示，小明选定场馆前的一棵树CD来测量，他先调整测倾器的位置发现，在H处观测树顶C的仰角为30°，此时恰好看到场馆AB的顶部A（G，C、A三点在一条直线上）；接着，小明从H处出发沿HB方向前进26m到达F处，此时观测树顶C的仰角为60°，测得BD＝60m，测倾器的高度GH＝EF＝1m，已知AB⊥BH，CD⊥BH，EF⊥BH，CH⊥BH，点D、F在BH上，求西安奥体中心主体育场馆AB的高度.（结果保留根号）

答案解析收藏纠错 + 选题
22. (2023九上·扶沟期末) 某饮料批发商店平均每天可售出某款饮料300瓶，售出1瓶该款饮料的利润是1元.经调查发现，若该款饮料的批发价每降低0.1元，则每天可多售出100瓶.为了使每天获得的利润更多，该饮料批发商店决定降价 $\text{[math]}$ 元．
1. （1）当 $\text{[math]}$ 为多少时，该饮料批发商店每天卖出该款饮料的利润为400元？
2. （2）该饮料批发商店每天卖出该款饮料的利润能达到600元吗？若能，请求出 $\text{[math]}$ 的值，若不能，请说明理由．
答案解析收藏纠错 + 选题
23. (2023九上·扶沟期末) 如图，直线 $\text{[math]}$ 交y轴于点A，交x轴于点B，抛物线 $\text{[math]}$ 经过点A，点B，且交x轴于另一点C.
1. （1）求点A，点B，点C的坐标并求抛物线的解析式；
2. （2）在直线 $\text{[math]}$ 上方的抛物线上有一点P，求四边形 $\text{[math]}$ 面积的最大值及此时点P的坐标；
3. （3）将线段 $\text{[math]}$ 绕x轴上的动点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 得到线段 $\text{[math]}$ ，若线段 $\text{[math]}$ 与抛物线只有一个公共点，请结合函数图象，求t的取值范围.
答案解析收藏纠错 + 选题