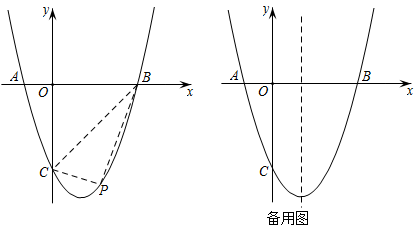
B .
B .  C .
C .  D .
D . 

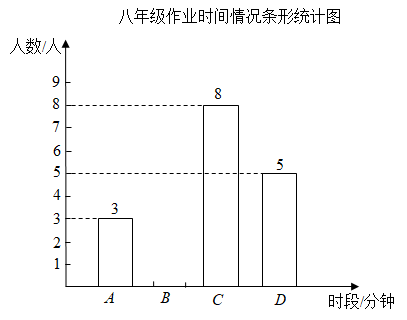
七年级取20名完成作业时间:55,58,60,65,64,66,60,60,78,78,70,75,75,78,78,80,82,85,85,88.
八年级抽取20名同学中完成作业时间在C时段的所有数据为:72,75,74,76,75,75,78,75.
七,八年级抽取的同学完成作业时间统计表:
年级 | 平均数 | 中位数 | 众数 |
七年级 | 72 | 75 | b |
八年级 | 75 | a | 75 |
根据以上信息,回答下列问题:
例如:∵ , 6比7小1,
, ∴4819是“双十数”;
又如:∵ , 3比4小1,
, ∴1496不是“双十数”.