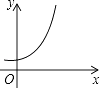 B .
B . 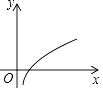 C .
C . 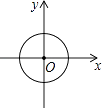 D .
D . 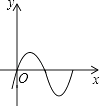
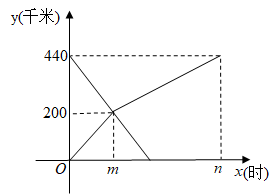
①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x,其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是( )

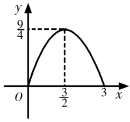 B .
B . 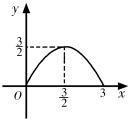 C .
C . 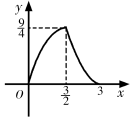 D .
D . 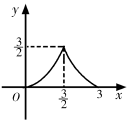
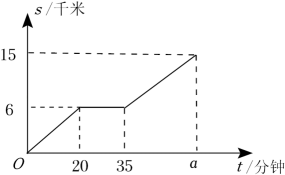
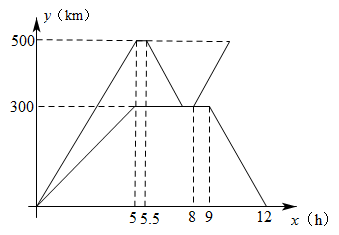
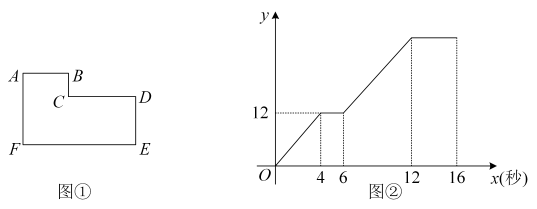
①体育场离王强家
②王强在体育场锻炼了
③王强吃早餐用了
④王强骑自行车的平均速度是

|
t小时 |
0.2 |
0.6 |
0.8 |
|
s千米 |
20 |
60 |
80 |
①列表:下列是x与y的几组对应值,其中a= ▲ .
x | …… | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 1 | 2 | 3 | 4 | 5 | …… |
y | …… | ﹣3.8 | ﹣2.5 | ﹣1 | 1 | 5 | 5 | a | ﹣1 | ﹣2.5 | ﹣3.8 | …… |
②描点:根据表中的数值描点(x,y),请补充描出点(2,a);
③连线:请用平滑的曲线顺次连接各点,画出函数图象;
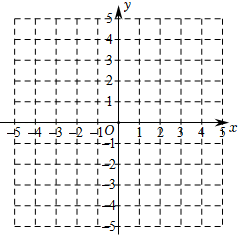
①写出方程-|x|=5的解;
②写出不等式-|x|≤1的解集.
时间x(天) | 3 | 5 | 6 | 9 | …… |
硫化物的浓度y(mg/L) | 4.5 | 2.7 | 2.25 | 1.5 | …… |

|
x(h) |
… |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
… |
|
Y(cm |
… |
189 |
137 |
103 |
80 |
101 |
133 |
202 |
260 |
… |
(数据来自某海洋研究所)
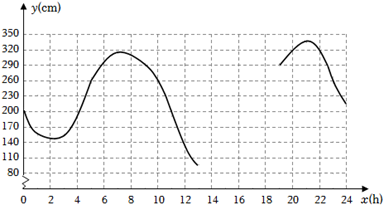
①根据表中数据,通过描点、连线(光滑曲线)的方式补全该函数的图象.
②观察函数图象,当x=4时,y的值为多少?当y的值最大时,x的值为多少?
请结合函数图象,写出该函数的两条性质或结论.
根据研究,当潮水高度超过260cm时,货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口?