浙江省金华市部分学校2022-2023学年八年级上学期期末数...

更新时间：2023-02-20 浏览次数：131 类型：期末考试

一、单选题

1. (2022八上·肇庆期末) 2022年冬奥会将在北京举行，中国将是第一个实现奥运“全满贯”（先后举办奥运会、残奥会、青奥会、冬奥会、冬残奥会）的国家，在会徽的图案设计中，设计者常常利用对称性进行设计，下列四个图案是历届会徽图案上的一部分图形，其中不是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2023八上·金华期末) 高钙牛奶的包装盒上注明“每100克内含钙≥150毫克”，它的含义是指（）

A . 每100克内含钙150毫克 B . 每100克内含钙高于150毫克 C . 每100克内含钙不低于150毫克 D . 每100克内含钙不超过150毫克

答案解析收藏纠错 + 选题
3. (2023八上·金华期末) 乐乐要从下面四组木棒中选择一组制作一个三角形作品，你认为他应该选（）

A . 3，5，6 B . 2，3，5 C . 2，4，7 D . 3，8，4

答案解析收藏纠错 + 选题
4. (2023八上·镇海区期末) 下列图形中，不能表示 $\text{[math]}$ 是 $\text{[math]}$ 函数的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024八上·岑溪期末) 已知 $\text{[math]}$ 都在直线 $\text{[math]}$ 上，则 $\text{[math]}$ 的值的大小关系是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023八上·金华期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 平分 $\text{[math]}$ ，交 $\text{[math]}$ 于点D，若点D恰好在边 $\text{[math]}$ 的垂直平分线上，则∠C的度数为（）

A . 30 B . 36 C . 40 D . 45

答案解析收藏纠错 + 选题
7. (2023八上·金华期末) 下列命题中，真命题的个数有（）个
①有一个角为 $\text{[math]}$ 的三角形是等边三角形；②底边相等的两个等腰三角形全等；③有一个内角是 $\text{[math]}$ 且腰长相等的两个等腰三角形全等；④一边上的中线等于这条边的一半的三角形是直角三角形．

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
8. (2023八上·台州期中) 如图，在△ABC中，作BC边上的高线，下列画法正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
9. (2023八上·金华期末) 如图，在平面直角坐标系中，已知点A（0，2），点B在第一象限内， $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 绕点O逆时针旋转，每次旋转 $\text{[math]}$ ，则第2022次旋转后，点B的坐标为（）

A . （ $\text{[math]}$ ， 3） B . （ $\text{[math]}$ ， 0） C . （ $\text{[math]}$ ， 3） D . （ $\text{[math]}$ ， 0）

答案解析收藏纠错 + 选题
10. (2023八上·金华期末) 将一个等腰三角形 $\text{[math]}$ 纸板沿垂线段 $\text{[math]}$ ， $\text{[math]}$ 进行剪切，得到三角形 $\text{[math]}$ ，再按如图2方式拼放，其中 $\text{[math]}$ 与 $\text{[math]}$ 共线.若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 7

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·宝安月考) 若x是非正数，则x0.（填不等号）

答案解析收藏纠错 + 选题
12. (2023八下·射洪月考) 已知y关于x的函数 $\text{[math]}$ 是正比例函数，则m的值是.

答案解析收藏纠错 + 选题
13. (2023八上·金华期末) 已知 $\text{[math]}$ ， $\text{[math]}$ ，那么以a、b为边长的直角三角形斜边上的中线长为 .

答案解析收藏纠错 + 选题
14. (2023八上·金华期末) 如图，在 $\text{[math]}$ 中，过点B作 $\text{[math]}$ 的角平分线 $\text{[math]}$ 的垂线，垂足为F， $\text{[math]}$ 交 $\text{[math]}$ 于点G，若 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为 .

答案解析收藏纠错 + 选题
15. (2023八上·金华期末) 运行程序如图所示，规定：从“输入一个值 $\text{[math]}$ ”到“结果是否 $\text{[math]}$ ”为一次程序操作，如果程序操作进行了三次才停止，那么 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
16. (2023八上·金华期末) 直线 $\text{[math]}$ 恒过一定点，则该点的坐标是．平面直角坐标系中有三点 $\text{[math]}$ ，若该直线 $\text{[math]}$ 将 $\text{[math]}$ 分成左右面积之比为1∶2的两部分，则k的值是．

答案解析收藏纠错 + 选题

三、解答题

17. (2023八上·金华期末) 解答下列各题：
1. （1）解不等式 $\text{[math]}$ ；
2. （2）把点A（a ，－3）向左平移3个单位，所得的点与点A关于y轴对称，求a的值.
答案解析收藏纠错 + 选题
18. (2023八上·金华期末) 如图，在△ABC中，D是AB上一点，CF//AB，DF交AC于点E， $\text{[math]}$ .
1. （1）求证： $\text{[math]}$
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求BD的长.
答案解析收藏纠错 + 选题
19. (2023八上·金华期末) 图①、图②均是4×4的正方形网格，每个小正方形的边长均为1，每个小正方形的顶点叫做格点，△ABC的顶点均在格点上，只用无刻度的直尺，在给定的网格中按要求
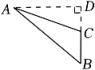
画图，不要求写出画法，保留作图痕迹.
1. （1）在图①中画△ABC的角平分线BD，标出点D；
2. （2）在图②中的边BC上找到格点E，连接AE，使AE平分△ABC的面积
答案解析收藏纠错 + 选题
20. (2023八上·金华期末) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ .
①分别以点A、B为圆心，以大于 $\text{[math]}$ 的长度为半径作弧，分别交于两点，连接这两点的直线与 $\text{[math]}$ 交于点D，与 $\text{[math]}$ 交于点F，连结 $\text{[math]}$ ；
②以点A为圆心，任意长为半径作弧，分别与 $\text{[math]}$ 、 $\text{[math]}$ 交于两点，再以这两点为圆心，以大于这两点间距离的一半的长度为半径作弧，两弧交于一点，连结点A与这一点交 $\text{[math]}$ 于点E.
1. （1）通过以上作图，可以发现直线 $\text{[math]}$ 是，射线 $\text{[math]}$ 是；（在横线上填上合适的选项）
  A.线段 $\text{[math]}$ 的垂直平分线 B. $\text{[math]}$ 的角平分线
  C. $\text{[math]}$ 的中线 D. $\text{[math]}$ 的角平分线
2. （2）在（1）所作的图中，求 $\text{[math]}$ 的度数.
答案解析收藏纠错 + 选题
21. (2023八上·金华期末) 某医药研究所开发了一种新药，在实验药效时发现，如果成人按规定剂量服用后，每毫升血液中含药量y（微克）随时间x（时）的变化情况如图所示，根据图象回答下列问题：
1. （1）求2≤x≤9时，y与x的函数表达式；
2. （2）如果每毫升血液中含药量为3.5微克及以上时治疗疾病有效，请问病人服药后9小时内有多长时间药物对治疗疾病有效？并说明理由.
答案解析收藏纠错 + 选题
22. (2023八上·台州期中) 如图，在△ABC中，∠ABC＝2∠ACB，BD为△ABC的角平分线；
1. （1）若AB＝BD，则∠A的度数为 °（直接写出结果）；
2. （2）如图1，若E为线段BC上一点，∠DEC＝∠A；求证：AB＝EC.
3. （3）如图2，若E为线段BD上一点，∠DEC＝∠A，求证：AB＝EC.
答案解析收藏纠错 + 选题
23. (2023八上·金华期末) 某商业集团准备购进A，B两款口袋打印机在甲、乙两个商场进行销售，这两款口袋打印机每台的利润如表：
打印机利润商场
甲商场
乙商场
A款（元/台）
95
60
$\text{[math]}$ 款（元/台）
70
45
为迎接双十二，该商业集团新进了40台A款，60台B款调配给甲，乙两个商场，其中70台给甲商场，30台给乙商场．
1. （1）设该集团调配给甲商场A款x台，求总利润y与x的函数关系式．
2. （2） ①若这100台口袋打印机全部销售出去，如何调配才能让商业集团的利润最大，并求出利润的最大值．
  ②为了促销，该商业集团决定对甲商场的A款，B款每台分别让利a元和b元（ $\text{[math]}$ ），其他销售利润不变，当天结算时发现销售总利润与调配方案无关．当总利润最大时，求此时a的值．
答案解析收藏纠错 + 选题
24. (2023八上·榆树期中) 如图，在平面直角坐标系中，直线 $\text{[math]}$ ： $\text{[math]}$ 交y轴于点A，交x轴于点B（4，0），过点E（2，0）的直线 $\text{[math]}$ 平行于y轴，交直线 $\text{[math]}$ 于点D，点P是直线 $\text{[math]}$ 上一动点（异于点D），连接 $\text{[math]}$ 、 $\text{[math]}$ .
1. （1）直线 $\text{[math]}$ 的表达式为，点D的坐标为；
2. （2）设P（2，m），当点P在点D的下方时，求 $\text{[math]}$ 的面积S的表达式（用含m的代数式表示）；
3. （3）当 $\text{[math]}$ 的面积为3时，则以点B为直角顶点作等腰直角 $\text{[math]}$ ，请直接写出点C的坐标.
答案解析收藏纠错 + 选题