山西省太原市2023届高三上学期数学期末试卷

更新时间：2023-02-24 浏览次数：35 类型：期末考试

一、单选题

1. (2023高三上·太原期末) 已知集合 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023高三上·太原期末) 设复数 $\text{[math]}$ 满足 $\text{[math]}$ 为虚数单位），则复数 $\text{[math]}$ 在复平面内所对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2023高三上·太原期末) 已知 $\text{[math]}$ ，则向量 $\text{[math]}$ 与 $\text{[math]}$ 的夹角为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023高三上·太原期末) 中国古代数学的瑰宝《九章算术》中记载了一种称为“曲池”的几何体，该几何体是上、下底面均为扇环形的柱体（扇环是指圆环被扇形截得的部分）．现有一个如图所示的曲池， $\text{[math]}$ 垂直于底面， $\text{[math]}$ ， $\text{[math]}$ ，底面扇环所对的圆心角为 $\text{[math]}$ ，弧 $\text{[math]}$ 的长度是弧 $\text{[math]}$ 长度的2倍， $\text{[math]}$ ，则该曲池的体积为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023高三上·太原期末) 某学校音乐社团为庆祝学校百年华诞将举办歌曲展演，要从4首独唱歌曲和2首合唱歌曲中选出4首歌曲安排演出，若最后一首歌曲必须是合唱歌曲，则不同的安排方法种数为（）

A . 96 B . 120 C . 240 D . 360

答案解析收藏纠错 + 选题
6. (2023高三上·太原期末) 已知 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023高三上·太原期末) 如表所示的数阵称为“森德拉姆素数筛”，表中每行每列的数都成等差数列，设 $\text{[math]}$ 表示该数阵中第m行、第n列的数，则下列说法正确的是（）
2
3
4
5
6
7
…
3
5
7
9
11
12
…
4
7
10
13
16
19
…
5
9
13
17
21
25
…
6
11
1
21
26
31
…
7
13
19
25
31
37
…
…
…
…
…
…
…
…

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023高三上·太原期末) 已知函数 $\text{[math]}$ 及其导函数 $\text{[math]}$ 的定义域均为 $\text{[math]}$ ，记 $\text{[math]}$ ，若 $\text{[math]}$ 均为偶函数，当 $\text{[math]}$ 时， $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 20 B . 30 C . 35 D . 40

答案解析收藏纠错 + 选题

二、多选题

9. (2023高三上·太原期末) 已知正数x，y满足 $\text{[math]}$ ，则下列结论正确的是（）

A . $\text{[math]}$ 的最大值是1 B . $\text{[math]}$ 的最小值是4 C . $\text{[math]}$ 的最大值是 $\text{[math]}$ D . $\text{[math]}$ 的最小值是1

答案解析收藏纠错 + 选题
10. (2023高三上·太原期末) 已知函数 $\text{[math]}$ 的部分图像如图所示，下列结论正确的是（）

A . $\text{[math]}$ 的图像关于直线 $\text{[math]}$ 对称 B . $\text{[math]}$ 的图像关于点 $\text{[math]}$ 对称 C . 将函数 $\text{[math]}$ 的图像向左平移 $\text{[math]}$ 个单位长度可以得到函数 $\text{[math]}$ 的图像 D . 方程 $\text{[math]}$ 在 $\text{[math]}$ 上有7个不相等的实数根

答案解析收藏纠错 + 选题
11. (2023高三上·太原期末) 已知抛物线 $\text{[math]}$ 的焦点为 $\text{[math]}$ ，过点 $\text{[math]}$ 的直线交 $\text{[math]}$ 于 $\text{[math]}$ 两个不同点，则下列结论正确的是（）

A . 若点 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值是3 B . $\text{[math]}$ 的最小值是2 C . 若 $\text{[math]}$ ，则直线 $\text{[math]}$ 的斜率为 $\text{[math]}$ D . 过点 $\text{[math]}$ 分别作抛物线 $\text{[math]}$ 的切线，设两切线的交点为 $\text{[math]}$ ，则点 $\text{[math]}$ 的横坐标为-1

答案解析收藏纠错 + 选题
12. (2023高三上·太原期末) 已知正四棱柱 $\text{[math]}$ 的底面边长为2，侧棱 $\text{[math]}$ ， P为上底面 $\text{[math]}$ 上的动点，M为棱 $\text{[math]}$ 的中点，下列结论正确的是（）

A . 三棱锥 $\text{[math]}$ 的体积为定值1 B . 当直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角为 $\text{[math]}$ 时，点P的轨迹长度为 $\text{[math]}$ C . 若直线 $\text{[math]}$ $\text{[math]}$ 平面 $\text{[math]}$ ，则线段 $\text{[math]}$ 长度的最小值为 $\text{[math]}$ D . 直线 $\text{[math]}$ 被正四棱柱 $\text{[math]}$ 外接球所截得线段长度的取值范围是 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题

13. (2023高三上·太原期末) 已知函数 $\text{[math]}$ 的图象在 $\text{[math]}$ 处的切线经过坐标原点，则实数 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2023高三上·太原期末) $\text{[math]}$ 的展开式中常数项为．（用数字作答）

答案解析收藏纠错 + 选题
15. (2023高三上·太原期末) 在临床上，经常用某种试验来诊断试验者是否患有某种癌症，设 $\text{[math]}$ “试验结果为阳性”， $\text{[math]}$ “试验者患有此癌症”，据临床统计显示 $\text{[math]}$ ， $\text{[math]}$ ．已知某地人群中患有此种癌症的概率为0.001，现从该人群中随机抽在了1人，其试验结果是阳性，则此人患有此种癌症的概率为．

答案解析收藏纠错 + 选题
16. (2023高三上·太原期末) 已知双曲线 $\text{[math]}$ 的左、右焦点分别为 $\text{[math]}$ ，过 $\text{[math]}$ 作圆 $\text{[math]}$ 的切线，切点为 $\text{[math]}$ ，延长 $\text{[math]}$ 交双曲线 $\text{[math]}$ 的左支于点 $\text{[math]}$ ．若 $\text{[math]}$ ，则双曲线 $\text{[math]}$ 离心率的取值范围是．

答案解析收藏纠错 + 选题

四、解答题

17. (2023高三上·太原期末) 已知数列 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ．
1. （1）从条件①、条件②这两个条件中选择一个条件作为已知，求 $\text{[math]}$ 的通项公式；
2. （2）设 $\text{[math]}$ ，记 $\text{[math]}$ 的前n项和为 $\text{[math]}$ ，若对任意正整数的n，不等式 $\text{[math]}$ 恒成立，求 $\text{[math]}$ 的最小值．
  条件① $\text{[math]}$ ，且 $\text{[math]}$ ；条件② $\text{[math]}$ 为等比数列，且满足 $\text{[math]}$ ；（注：若条件①和条件②分别解答，按第一个解答计分．）
答案解析收藏纠错 + 选题
18. (2023高三上·太原期末) 在 $\text{[math]}$ 中，内角 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 所对的边分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且满足 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
19. (2023高三上·太原期末) 从某企业生产的某种产品中抽取500件，测量这些产品的一项质量指标值，整理测量结果得到如下频率分布直方图：
1. （1）求这500件产品质量指标值的样本平均值 $\text{[math]}$ 和样本方差 $\text{[math]}$ （同一组的数据用该组区间的中点值作代表）；
2. （2）由直方图可以认为，这种产品的质量指标Z服从正态分布 $\text{[math]}$ ，其中 $\text{[math]}$ 近似为样本平均数 $\text{[math]}$ 近似为样本方差 $\text{[math]}$ ．
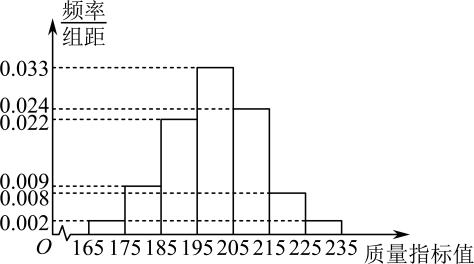
  （ⅰ）利用该正态分布，求 $\text{[math]}$ ；
  （ⅱ）某用户从该企业购买了100件这种产品，记X表示这100件产品中质量指标值位于区间 $\text{[math]}$ 的产品件数．利用（ⅰ）的结果，求 $\text{[math]}$ ．
  附： $\text{[math]}$ ；若 $\text{[math]}$ ，则 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2023高三上·太原期末) 如图，在三棱锥 $\text{[math]}$ 中，平面 $\text{[math]}$ 平面 $\text{[math]}$ ， $\text{[math]}$ ， O为 $\text{[math]}$ 的中点．
1. （1）证明： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 是边长为1的等边三角形，点E在棱 $\text{[math]}$ 上， $\text{[math]}$ ，且二面角 $\text{[math]}$ 的大小为 $\text{[math]}$ ，求直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值．
答案解析收藏纠错 + 选题
21. (2023高三上·太原期末) 已知椭圆 $\text{[math]}$ 的左右焦点分别为 $\text{[math]}$ ，椭圆C经过点 $\text{[math]}$ ，且直线 $\text{[math]}$ ，与圆 $\text{[math]}$ 相切．
1. （1）求椭圆C的方程；
2. （2）直线 $\text{[math]}$ 与椭圆C交于P，Q两点，点M在x轴上，且满足 $\text{[math]}$ ，求点M横坐标的取值范围．
答案解析收藏纠错 + 选题
22. (2023高三上·太原期末) 已知函数 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ 在 $\text{[math]}$ 处取得极大值，求 $\text{[math]}$ 的单调区间；
2. （2）若 $\text{[math]}$ 恰有三个零点，求实数 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题