吉林省长春市2022年5月中考模拟——数学试卷

更新时间：2024-07-13 浏览次数：91 类型：中考模拟

一、选择题(本大题共8小题，每小题3分，共24分)

1. (2024九下·朝阳模拟) 互为相反数的两个数的和为（）

A . 0 B . 正数 C . 负数 D . 无法确定

答案解析收藏纠错 + 选题
2. (2022·长春模拟) 2022年3月23日下午，“天宫课堂”第二课在中国空间站开讲，由神舟十三号乘组航天员翟志刚、王亚平、叶光富在太空进行授课．央视新闻抖音号全程进行直播，观看人数达到3 150000人。其中3 150 000这个数用科学记数法表示为（）

A . 0.315×10⁷ B . 3.15×10⁶ C . 3.15×10⁷ D . 315×10⁴

答案解析收藏纠错 + 选题
3. (2022·长春模拟) 如图，在有序号的小正方形中选出一个，它与图中五个有阴影的小正方形组合后，不能构成正方体的表面展开图的是（）

A . ① B . ② C . ③ D . ④

答案解析收藏纠错 + 选题
4. (2022·长春模拟) 不等式3x>-3的解集在数轴上表示正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2022·长春模拟) 某书店拿取高处书籍的登高梯如图位置摆放，登高梯AC的顶端A恰好放在书架的第七层的顶端，已知登高梯的长度AC为3.2米，登高梯与地面的夹角∠ACB为73°，则书架第七层顶端离地面的高度AB为（）

A . 3.2cos73°米 B . $\text{[math]}$ 米 C . 3.2sin73°米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
6. (2022·长春模拟) 如图，在△ABC中，∠BAC=100°，∠ABC=26°，点D在边BC上，连结AD．当AD=AC时，∠ADC的大小为（）

A . 54° B . 56° C . 64° D . 74°

答案解析收藏纠错 + 选题
7. (2022·长春模拟) 如图，在 $\text{[math]}$ ABCD中，AB>AD，按如下步骤作图：①以点A为圆心，AD的长为半径作圆弧，交边AB于点E；②分别以点D和点E为圆心、大于线段DE长的一半为半径作圆弧，两弧交于点P；③作射线AP，交边CD于点F；④连结EF．下列结论不一定成立的是（）

A . AE=AD B . AF=AB C . EF=BC D . AD=DF

答案解析收藏纠错 + 选题
8. (2022·长春模拟) 如图，在平面直角坐标系中，反比例函数y= $\text{[math]}$ (k为常数)的图象与正比例函数y=x的图象交于A、B两点．若AB=2 $\text{[math]}$ ，则k的值为（）

A . 4 B . 2 $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题

二、填空题(本大题共6小题，每小题3分，共18分)

9. (2024九上·嘉峪关模拟) 分解因式： $\text{[math]}$ －9=．

答案解析收藏纠错 + 选题
10. (2022七下·宽城期末) 已知一个三角形的两边长分别为2和5，若第三边的长为整数，则第三边的长可以为(写出一个即可)

答案解析收藏纠错 + 选题
11. (2022·长春模拟) 《九章算术》是我国古代的数学名著，其中“勾股”章有一题，大意是说：矩形门的高比宽多6尺，门的对角线长为10尺，那么门的高和宽各是多少尺？如果设门的高为x尺，那么根据题意，可列方程为

答案解析收藏纠错 + 选题
12. (2022·长春模拟) 如图，点E、F分别是正方形ABCD的边AB、CD的中点，连结AF、BF、CE、DE，AF与DE相交于点G，BF与CE相交于点H．若AB=1，则四边形EHFG的面积为

答案解析收藏纠错 + 选题
13. (2022·长春模拟) 如图，在△ABC中，BC=5，点I为△ABC的内心。将△ABC平移到△IDE的位置，点A的对应点为点I，则图中阴影部分图形的周长为

答案解析收藏纠错 + 选题
14. (2022·长春模拟) 在平面直角坐标系中，抛物线y= $\text{[math]}$ x²-bx+c(b>0，b、c为常数)的顶点为A，与y轴交于点B，点B关于抛物线对称轴的对称点为C．若△ABC是等腰直角三角形，则BC的长为

答案解析收藏纠错 + 选题

三、解答题(本大题共10小题，共78分)

15. (2022·长春模拟) 先化简，再求值：m(m-4)+(m+2)²-1，其中m= $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2022·长春模拟) 如图，在4X4的正方形网格中，每个小正方形的边长均为1个单位长度，小正方形的顶点称为格点，点A、O均在格点上，小乌龟初始位于点O，它的每一步都会在以下三种情形中随机地选择一种：①向左移动1个单位长度(记为左)；②向上移动1个单位长度(记为上)；③向右移动1个单位长度(记为右) ．用画树状图(或列表)的方法，求小乌龟两步之后到达点A的概率．

答案解析收藏纠错 + 选题
17. (2022·长春模拟) 长春冰雪新天地是美丽春城的一道亮丽的风景线，它的设计和造型每年都有变化．在2021年长春冰雪新天地的建造过程中，某工程公司承担了为某项建设取600吨冰块的任务，由于任务紧急，实际取冰时的工作效率比原计划提高了20%，结果提前1天完成任务．该公司原计划每天取冰块多少吨？

答案解析收藏纠错 + 选题
18. (2022·长春模拟) 如图，在△ABC中，∠ACB=90°，AD平分∠BAC，交边BC于点D，O为边AB上一点，以点O为圆心，OA长为半径的圆恰好经过点D．
1. （1）求证： BC是⊙O的切线．
2. （2）若⊙O的半径为2，AC=3，则AB的长为
答案解析收藏纠错 + 选题
19. (2022·长春模拟) 初三学生小明就如何分配周末自主复习语文、数学、英语的时间问题，去请教了班主任．班主任结合小明本学期三次模拟考试的成绩，建议他根据“相对失分比”的情况，划分周末复习时间．
具体操作分为四步：
第一步：计算小明这三次模拟考试中语文、数学、英语单科成绩与当次考试该科年级最高分的差值作为“相对失分”，并记录如下：
小明这三次模拟考试中语文、数学、英语每科成绩“相对失分”表．
学科
相对失分
模拟次数
语文
数学
英语
第一次
15
13
5
第二次
8
14
7
和三次
13
9
6
第二步：计算表中每科成绩的“相对失分”的平均数，并分别记作： $\text{[math]}$ 语文， $\text{[math]}$ 数学， $\text{[math]}$ 英语；
第三步：计算表中每科成绩的“相对失分比”；
某一科成绩的“相对失分比”= $\text{[math]}$ ×100%
例：语文成绩的“相对失分比”= $\text{[math]}$ ×100%．
第四步：根据“相对失分比”划分复习时间，即某科的“相对失分比”就是该科周末复习时间的占比．
根据以上操作步骤，解答下列问题：
1. （1）小明的语文三次成绩“相对失分”的平均数 $\text{[math]}$ 语文=分．
2. （2）小明想通过扇形统计图直观地显示语文、数学、英语每科成绩“相对失分比”的情况，请分别计算小明这三科每科成绩的“相对失分比”，并绘制扇形统计图．
3. （3）假设小明周末复习语文、数学、英语三科的时间共有200分钟，那么按照上述方法，小明应分配给语文学科的复习时间约为分钟．
答案解析收藏纠错 + 选题
20. (2022·长春模拟) 图①、图②、图③分别是6×6的正方形网格，网格中每个小正方形的边长均为1，小正方形的顶点称为格点，点A、B、C、D、E、P、Q、M、N均在格点上，仅用无刻度的直尺在下列网格中按要求作图，保留作图痕迹．
1. （1）在图①中，画线段AB的中点F．
2. （2）在图②中，画△CDE的中位线GH，点G、H分别在线段CD、CE上，并直接写出△CGH与四边形DEHG的面积比．
3. （3）在图③中，画△PQR，点R在格点上，且△PQR被线段MN分成的两部分图形的面积比为1：3．
答案解析收藏纠错 + 选题
21. (2022·长春模拟) 已知A、B两地之间有一条笔直公路，甲车从A地出发匀速去往B地，到达B地后立即以原速原路返回A地，乙车从B地出发匀速去往A地，两车同时出发，乙车比甲车晚20分钟到达A地、甲车距A地的路程y(千米)与甲车行驶的时间x(分钟)之间的函数关系如图所示．
1. （1）在图中画出乙车距A地的路程y(千米)与x(分钟)之间的函数图象，并求出它所对应的函数关系式．(写出自变量x的取值范围)
2. （2）甲、乙两车在行驶过程中相遇了次．
3. （3）求甲车到B地时，乙车距A地的路程．
答案解析收藏纠错 + 选题
22. (2022·长春模拟) [问题呈现]小强在一次学习过程中遇到了下面的问题：
如图①，在△ABC与ODEF中，AB=DE，∠A=∠D，AC+BC=DF．
求证：∠ACB=2∠F．
1. （1） [方法探究]以下是小强的方法：
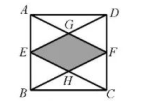
  证明：如图②，延长AC到点G，使CG=CB，连结BG．
  ∵CG=CB，
  ∴∠CBG=∠G ．
  ∴∠ACB=∠CBG+∠G=2∠G．
  接下来只需证明∠G=∠F，进而就能得出∠ACB=2∠F ．
  请你补全余下的证明过程．
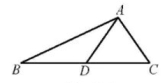
2. （2） [方法总结]从上面的方法可以看出，通过“化折为直”，不仅可以构造等腰三角形，还可以得到角的倍、半关系，可谓一举两得．
  [方法应用]如图③，在△ABC中，∠ACB=90°，∠A=35°，延长BC到点D，使DC=BC，点E在边AC上，连结DE．当DE+EC=AC时，∠DEC的大小为°
3. （3） [拓展延伸]如图④，在△ABC中，∠C=90°，∠B=50°．若AB+BC=10，求边AC的长．(精确到 0.1)
  [参考数据：sin25°≈0.423，cos25°≈ 0.906，tan25°≈0.466 ]
答案解析收藏纠错 + 选题
23. (2022·长春模拟) 如图， $\text{[math]}$ ABCD的面积为12，AB=6，AD=3．点M在边AB上(点M与点A不重合)，连结DM，作点A关于直线DM的对称点A'，连结AM、AD．
1. （1）点D到直线AB的距离是．
2. （2）设点A'到直线BC的距离为d，求d的最小值．
3. （3）当点A'落在 $\text{[math]}$ ABCD的边上时，求AM的长．
4. （4）当直线A'M与 $\text{[math]}$ ABCD的一边垂直时，直接写出AM的长．
答案解析收藏纠错 + 选题
24. (2022·长春模拟) 在平面直角坐标系中，抛物线y=x²+bx+c (b、c为常数)的对称轴为直线x=1，与y轴交点的坐标为(0，-2)，点A、点B均在这个抛物线上(点A在点B的左侧)，点A的横坐标为m，点B的横坐标为1-2m．
1. （1）求此抛物线对应的函数表达式．
2. （2）当点A、点B关于此抛物线的对称轴对称时，连结AB，求线段AB的长．
3. （3）将此抛物线上A、B两点之间的部分(包括A、B两点)记为图象G．
  ①当图象G对应的函数值y随x的增大而先减小后增大时，设图象G最高点的纵坐标与最低点的纵坐标的差为h，求h与m之间的函数关系式，并写出h的取值范围．
  ②设点E的坐标为(-2-2m，1)，点F的坐标为(-2-2m，-3-2m)，连结EF，当线段EF和图象G有公共点时，直接写出m的取值范围．
答案解析收藏纠错 + 选题