山西省忻州市原平市2023年中考一模数学试题

更新时间：2023-05-16 浏览次数：86 类型：中考模拟

一、单选题

1. (2023·原平模拟) -6的绝对值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·原平模拟) 如图所示的是由4个大小相同的小正方体搭建而成的几何体，则该几何体的左视图为（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2023·防城模拟) 2022年12月26日是伟大领袖毛主席诞辰129周年纪念日，伟人在他的诗词中写道“坐地日行八万里，巡天遥看一千河”，那么数据“八万里”用科学记数法可表示为（）

A . $\text{[math]}$ 里 B . $\text{[math]}$ 里 C . $\text{[math]}$ 里 D . $\text{[math]}$ 里

答案解析收藏纠错 + 选题
4. (2024九下·九江期中) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·原平模拟) 如图，五线谱是由等距离、等长度的五条平行横线组成的，同一条直线上的三个点A，B，C都在横线上，若线段 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长是（）

A . $\text{[math]}$ $\text{[math]}$ B . $\text{[math]}$ $\text{[math]}$ C . $\text{[math]}$ $\text{[math]}$ D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023·原平模拟) 将不等式组 $\text{[math]}$ 的解集在数轴上表示，正确的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
7. (2023·原平模拟) 小明坚持每天进行体育锻炼，如表是小明近一周的体育锻炼时间表：
日期
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
时间（分钟）
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
则这组数据的中位数和众数分别是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·原平模拟) 如图，点A，B，C均在⊙O上，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·原平模拟) 在2023年中考体育考试前，小康对自己某次实心球的训练录像进行了分析，发现实心球飞行路线是一条抛物线，若不考虑空气阻力，实心球的飞行高度y（单位：米）与飞行的水平距离x（单位：米）之间具有函数关系 $\text{[math]}$ ，则小康这次实心球训练的成绩为（）

A . 14米 B . 12米 C . 11米 D . 10米

答案解析收藏纠错 + 选题
10. (2023·原平模拟) 如图，四边形 $\text{[math]}$ 是菱形， $\text{[math]}$ ， $\text{[math]}$ ，扇形 $\text{[math]}$ 的半径为4，圆心角为 $\text{[math]}$ ，则图中阴影部分的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024八上·绥阳月考) 计算： $\text{[math]}$ =

答案解析收藏纠错 + 选题
12. (2023·原平模拟) 如图所示的是一组有规律的图案，则第n个图案中“”的个数为．（用含n的代数式表示）

答案解析收藏纠错 + 选题
13. (2023·原平模拟) 如图，直线 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于点A，B，与x轴交于点D，过点A作 $\text{[math]}$ 轴于点C，若 $\text{[math]}$ ，则k=．

答案解析收藏纠错 + 选题
14. (2023·原平模拟) $\text{[math]}$ 年元旦期间，小华和家人到汾河公园景区游玩，湖边有大小两种游船，小华发现：2艘大船与3艘小船一次共可以满载游客60人，1艘大船与1艘小船一次共可以满载游客 $\text{[math]}$ 人．则1艘大船可以满载游客的人数为．

答案解析收藏纠错 + 选题
15. (2023·原平模拟) 如图，在菱形 $\text{[math]}$ 中，边长为 $\text{[math]}$ ， $\text{[math]}$ ， E，F分别是边 $\text{[math]}$ 上的点，且 $\text{[math]}$ ，若将 $\text{[math]}$ 沿着 $\text{[math]}$ 折叠，使得点B恰好落在 $\text{[math]}$ 边上的点 $\text{[math]}$ 处， $\text{[math]}$ ，折痕为 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题

16. (2023·原平模拟)
1. （1）计算： $\text{[math]}$ ；
2. （2）解方程： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
17. (2023·防城模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ．
1. （1）以 $\text{[math]}$ 为直径，利用尺规作 $\text{[math]}$ 交 $\text{[math]}$ 于点D．（要求：尺规作图并保留作图痕迹，不写作法，标明字母）
2. （2）在（1）中所作的图中，若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的半径．
答案解析收藏纠错 + 选题
18. (2023·原平模拟) 布艺手袋因节能时尚，成为学生一族的新宠．该商店用1200元购进第一批布艺手袋，很快售罄，于是又花费4500元购进第二批布艺手袋，所购数量是第一批的2倍，已知第二批布艺手袋的单价比第一批布艺手袋的单价贵7元，求第一批购进的布艺手袋的单价．

答案解析收藏纠错 + 选题
19. (2023·原平模拟) 为了贯彻落实国务院提出的“健康第一”的指导思想，切实加强学校体育工作，使学生养成良好的锻炼习惯，提高学生体质的健康水平，《国家中学生体质健康标准》规定学生体质健康等级标准如表：
等级
A：优秀
B：良好
C：及格
D：不及格
分数（x/分）
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
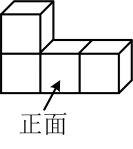
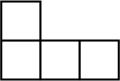
太原市某校从九年级学生中随机抽取了400名学生进行了体质测试，将调查结果整理后绘制成如图所示的两幅统计图，根据统计图提供的信息解答下列问题：
1. （1）在这被抽查的九年级学生中，优秀的有人，及格的有人．
2. （2）求所抽取的400名学生的平均分．
3. （3）该校校委会决定从获得优秀奖成绩前三名学生中选取2名同学参加省体质测试，已知前三名学生中只有1名男生，请用列表或画树状图的方法求所选的2名学生恰好是1名男生和1名女生的概率．
答案解析收藏纠错 + 选题

20. (2023·原平模拟) 阅读与思考．

纯几何法验证勾股定理我们知道，勾股定理：在直角三角形中，两条直角边的平方和等于斜边的平方．勾股定理的验证方法到目前为止也有300多种，最著名的有“赵爽弦图法”“总统证法”“毕达哥拉斯法”“青朱出入法”“达·芬奇法”“欧几里得法”等等．下面我们介绍一种纯几何验证法．

如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 于点D，先证明 $\text{[math]}$ ，可得 $\text{[math]}$ ，再证明 $\text{[math]}$ ，可得 $\text{[math]}$ ，两式相加即可得勾股定理，这种方法避开了利用拼图和面积法繁琐的证明，不失为一种很好的验证方法．

阅读下列材料，并完成相应的任务．

（1）根据材料中的方法，请写出完整的证明过程．
（2）如图2，将直角三角形分割成一个正方形和两对全等的直角三角形，我们把这样的直角三角形称为“勾股形”，图3是由两个完全相同的“勾股形”拼接而成的矩形，若 $\text{[math]}$ ，求该矩形的面积．

答案解析收藏纠错 + 选题

21. (2023·原平模拟) 如图1所示的是一种太阳能路灯，它由灯杆和灯管支架两部组成，图2是它的简易平面图．小明想知道灯管 $\text{[math]}$ 距地面 $\text{[math]}$ 的高度，他在地面 $\text{[math]}$ 处测得灯管 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，在地面 $\text{[math]}$ 处测得在灯管 $\text{[math]}$ 仰角为 $\text{[math]}$ ，并测得 $\text{[math]}$ ，已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 在同一条直线上，请根据以上数据帮小明算出灯管 $\text{[math]}$ 距地面 $\text{[math]}$ 的高度（结果精确到 $\text{[math]}$ ，参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）．

答案解析收藏纠错 + 选题
22. (2023·原平模拟)
1. （1）综合与实践
  问题情境：如图1，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， D，E分别是 $\text{[math]}$ ， $\text{[math]}$ 的中点，连接 $\text{[math]}$ ．
  如图2，将 $\text{[math]}$ 绕着点C逆时针旋转 $\text{[math]}$ ，连接BE和 $\text{[math]}$ ，小明发现 $\text{[math]}$ ， $\text{[math]}$ ，请你证明该结论．
2. （2）猜想探究：
  如图3，将 $\text{[math]}$ 绕着点C逆时针旋转 $\text{[math]}$ ，此时恰好有 $\text{[math]}$ ，连接 $\text{[math]}$ ，延长 $\text{[math]}$ ，交 $\text{[math]}$ 于点F，试猜想四边形 $\text{[math]}$ 的形状，并说明理由．
  拓展探究：
3. （3）如图4，将 $\text{[math]}$ 绕着点C逆时针旋转 $\text{[math]}$ ，直接写出四边形 $\text{[math]}$ 的面积的最大值．
答案解析收藏纠错 + 选题
23. (2023·原平模拟) 综合与探究．
如图1，抛物线 $\text{[math]}$ 经过 $\text{[math]}$ ， $\text{[math]}$ ，且与x轴交于A，B两点（点B在点A的右侧），与y轴交于点C，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求抛物线的表达式．
2. （2）求证： $\text{[math]}$ ．
3. （3）如图2，动点P从点B出发，沿着线段 $\text{[math]}$ 以每秒1个单位长度的速度向终点A运动；同时，动点Q从点A出发，以相同的速度沿着线段 $\text{[math]}$ 向终点C运动，当其中一个动点到达终点时，另一个动点也随之停止运动，连接 $\text{[math]}$ ，设P，Q运动的时间为t秒，在点P，Q运动的过程中， $\text{[math]}$ 是否成为等腰三角形？若能，请求出t的值；若不能，请说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

山西省忻州市原平市2023年中考一模数学试题

副标题：

*注意事项：

山西省忻州市原平市2023年中考一模数学试题

试题分析

总体分析

题量分析

难度分析

知识点分析

日期	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
时间（分钟）	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

等级	A：优秀	B：良好	C：及格	D：不及格
分数（x/分）	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$