湖北省荆州市2023年中考数学试卷

更新时间：2023-07-03 浏览次数：188 类型：中考真卷

一、选择题（本大题共有10个小题，每小题只有唯一正确答案，每小题3分，共30分）

1. (2024·从江模拟) 在实数－1， $\text{[math]}$ ， $\text{[math]}$ ， 3.14中，无理数是（）

A . －1 B . $\text{[math]}$ C . $\text{[math]}$ D . 3.14

答案解析收藏纠错 + 选题
2. (2024九下·长寿期中) 下列各式运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024·冠县模拟) 观察如图所示的几何体，下列关于其三视图的说法正确的是（）

A . 主视图既是中心对称图形，又是轴对称图形 B . 左视图既是中心对称图形，又是轴对称图形 C . 俯视图既是中心对称图形，又是轴对称图形 D . 主视图、左视图、俯视图都是中心对称图形

答案解析收藏纠错 + 选题
4. 已知蓄电池的电压U为定值，使用蓄电池时，电流I（单位：A)与电阻R（单位：Ω）是反比例函数关系（ $\text{[math]}$ )．下列反映电流I与电阻R之间函数关系的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2024九下·邯山模拟) 已知 $\text{[math]}$ ，则与 $\text{[math]}$ 最接近的整数为（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
6. 为评估一种水稻的种植效果，选了10块地作试验田．这10块地的亩产量（单位：kg）分别为x₁ ， x₂ ， …，x₁₀ ，下面给出的统计量中可以用来评估这种水稻亩产量稳定程度的是（）

A . 这组数据的平均数 B . 这组数据的方差 C . 这组数据的众数 D . 这组数据的中位数

答案解析收藏纠错 + 选题
7. (2023·荆州) 如图所示的“箭头”图形中，AB∥CD， $\text{[math]}$ ，则图中∠G的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023·荆州) 我国古代数学名著《孙子算经》中记载：“今有木，不知长短，引绳度之，余绳四尺五寸；屈绳量之，不足一尺，木长几何？”意思是：用一根绳子去量一根木条，绳子还余4.5尺；将绳子对折再量木条，木条余1尺，问木条长多少尺？若设木条长x尺，绳子长y尺，则可列方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023·荆州) 如图，直线 $\text{[math]}$ 分别与x轴，y轴交于点A，B，将△OAB绕着点A顺时针旋转 $\text{[math]}$ 得到△CAD，则点B的对应点D的坐标是（）

A . （2，5） B . （3，5） C . （5，2） D . （ $\text{[math]}$ ， 2）

答案解析收藏纠错 + 选题
10. (2023·荆州) 如图，一条公路的转弯处是一段圆弧（ $\text{[math]}$ ），点O是这段弧所在圆的圆心，B为 $\text{[math]}$ 上一点，OB⊥AC于D. 若AC= $\text{[math]}$ m，BD=150m，则 $\text{[math]}$ 的长为（）

A . $\text{[math]}$ m B . $\text{[math]}$ m C . $\text{[math]}$ m D . $\text{[math]}$ m

答案解析收藏纠错 + 选题

二、填空题（本大题共6个小题，每小题3分，共18分）

11. 若 $\text{[math]}$ ，则 $\text{[math]}$ =．

答案解析收藏纠错 + 选题
12. (2024·珠海模拟) 如图，CD为Rt△ABC斜边AB上的中线，E为AC的中点．若 $\text{[math]}$ ， $\text{[math]}$ ，则DE=．

答案解析收藏纠错 + 选题
13. (2024六上·济宁期末) 某校为了解学生对A，B，C，D四类运动的参与情况，随机调查了本校80名学生，让他们从中选择参与最多的一类，得到对应的人数分别是30，20，18，12．若该校有800名学生，则估计有人参与A类运动最多．

答案解析收藏纠错 + 选题
14. (2023·荆州) 如图，∠AOB=60^o ，点C在OB上，OC= $\text{[math]}$ ， P为∠AOB内一点．根据图中尺规作图痕迹推断，点P到OA的距离为．

答案解析收藏纠错 + 选题
15. (2023·荆州) 如图，无人机在空中A处测得某校旗杆顶部B的仰角为30^o ，底部C的俯角为60^o ，无人机与旗杆的水平距离AD为6m，则该校的旗杆高约为m．（ $\text{[math]}$ ，结果精确到0.1）

答案解析收藏纠错 + 选题
16. 如图，点A（2，2）在双曲线 $\text{[math]}$ 上，将直线OA向上平移若干个单位长度交y轴于点B，交双曲线于点C. 若BC=2，则点C的坐标是．

答案解析收藏纠错 + 选题

三、解答题（本大题共有8个小题，共72分）

17. (2023·荆州) 先化简，再求值：
$\text{[math]}$ ，其中 $\text{[math]}$

答案解析收藏纠错 + 选题
18. 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个不相等的实数根．
1. （1）求 $\text{[math]}$ 的取值范围；
2. （2）当 $\text{[math]}$ 时，用配方法解方程．
答案解析收藏纠错 + 选题
19. (2023·荆州) 如图，BD是等边△ABC的中线，以D为圆心，DB的长为半径画弧，交BC的延长线于E，连接DE．求证：CD=CE．

答案解析收藏纠错 + 选题

20. (2023九上·平阴期中) 首届楚文化节在荆州举办前，主办方为使参与服务的志愿者队伍整齐，随机抽取了部分志愿者，对其身高进行调查，将身高（单位：cm）数据分A，B，C，D，E五组制成了如下的统计图表（不完整）．

组别	身高分组	人数
A	155≤x＜160	3
B	160≤x＜165	2
C	165≤x＜170	m
D	170≤x＜175	5
E	175≤x＜180	4

根据以上信息回答：

（1）这次被调查身高的志愿者有人，表中的 $\text{[math]}$ ，扇形统计图中α的度数是；
（2）若E组的4人中，男女各有2人，以抽签方式从中随机抽取两人担任组长．请列表或画树状图，求刚好抽中两名女志愿者的概率．

答案解析收藏纠错 + 选题

21. (2023·荆州) 如图，在菱形ABCD中， $\text{[math]}$ 于H，以DH为直径的⊙O分别交AD，BD于点E，F，连接EF．
1. （1）求证：①CD是⊙O的切线；②△DEF∽△DBA；
2. （2）若AB=5，DB=6 ，求 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
22. (2024九下·蓬莱模拟) 荆州古城旁“荆街”某商铺打算购进A，B两种文创饰品对游客销售．已知1400元采购A种的件数是630元采购B种件数的2倍，A种的进价比B种的进价每件多1元，两种饰品的售价均为每件15元；计划采购这两种饰品共600件，采购B种的件数不低于390件，不超过A种件数的4倍．
1. （1）求A，B饰品每件的进价分别为多少元？
2. （2）若采购这两种饰品只有一种情况可优惠，即一次性采购A种超过150件时，A种超过的部分按进价打6折．设购进A种饰品x件，①求x的取值范围；②设计能让这次采购的饰品获利最大的方案，并求出最大利润．
答案解析收藏纠错 + 选题
23. (2023·荆州) 如图1，点P是线段AB上与点A，点B不重合的任意一点，在AB的同侧分别以A，P，B为顶点作 ∠1=∠2=∠3，其中∠1与∠3的一边分别是射线AB和射线BA，∠2的两边不在直线AB上，我们规定这三个角互为等联角，点P为等联点，线段AB为等联线．
1. （1）如图2，在5×3个方格的纸上，小正方形的顶点为格点、边长均为1，AB为端点在格点的已知线段．请用三种不同连接格点的方法，作出以线段AB为等联线、某格点P为等联点的等联角，并标出等联角，保留作图痕迹；
2. （2）如图3，在Rt△APC中，∠A=90°， $\text{[math]}$ ，延长AP至点B，使AB=AC，作∠A的等联角∠CPD和∠PBD．将△APC沿PC折叠，使点A落在点M处，得到△MPC，再延长PM交BD的延长线于E，连接CE并延长交PD的延长线于F，连接BF．
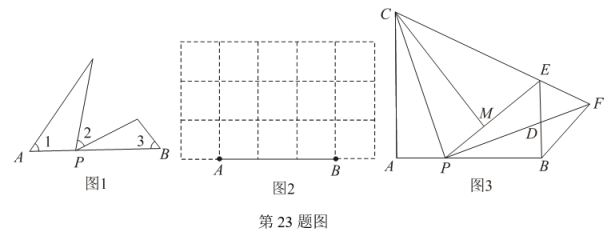
  ①确定△PCF的形状，并说明理由；
  
  ②若AP：PB=1：2，BF= $\text{[math]}$ k，求等联线AB和线段PE的长（用含k的式子表示）．
答案解析收藏纠错 + 选题
24. (2023·荆州) 已知：y关于x的函数 $\text{[math]}$ ．
1. （1）若函数的图象与坐标轴有两个公共点，且 $\text{[math]}$ ，则a的值是；
2. （2）如图，若函数的图象为抛物线，与x轴有两个公共点A（-2，0），B（4，0），并与动直线l： $\text{[math]}$ 交于点P，连接PA，PB，PC，BC，其中PA交y轴于点D，交BC于点E．设△PBE的面积为 $\text{[math]}$ ， △CDE的面积为 $\text{[math]}$ ．
  ①当点P为抛物线顶点时，求△PBC的面积；
  
  ②探究直线l在运动过程中， $\text{[math]}$ － $\text{[math]}$ 是否存在最大值？若存在，求出这个最大值；若不存在，说明理由．
答案解析收藏纠错 + 选题