
解:已知
,
( ).
▲
等量代换
.
( ).
▲ ( ).
平分
,
▲ ( ).
( ).
例如:解方程 .
解: ,
在数轴上与原点距离为
的点对应的数为
, 即该方程的解为
.
【理解应用】根据绝对值的几何意义可以解一些绝对值不等式.
我们定义:形如“ ,
,
,
”
为非负数
的不等式叫做绝对值不等式,能使一个绝对值不等式成立的所有未知数的值称为绝对值不等式的解集.

由图可以得出:绝对值不等式
的解集是
或
,
绝对值不等式的解集是
.
例如:解不等式 .
解:如图 , 首先在数轴上找出
的解,即到
的距离为
的点对应的数为
,
, 则
的解集为到
的距离大于
的点对应的所有数,所以原不等式的解集为
或
.
参考阅读材料,解答下列问题:
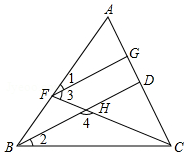
①是
的角平分线
判断:
填“是”或“不是”
“准直角三角形”;
②点是边
上一点,
是“准直角三角形”,若
, 则
的度数是.