（人教版）2023-2024学年九年级数学上册22.1 二次...

更新时间：2023-07-31 浏览次数：112 类型：同步测试

一、选择题

1. 已知菱形ABCD的边长为1，∠DAB=60°，E为AD上的动点，F在CD上，且AE+CF=1，设ΔBEF的面积为y，AE=x，当点E运动时，能正确描述y与x关系的图像是：（）

A . B . C . D .

答案解析收藏纠错 + 选题
2.
如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是( )

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023九上·邹城月考) 函数y=ax²与y=ax+b(a>0，b>0)在同一坐标系中的大致图象是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2022九上·广州月考) 若二次函数y＝（x﹣3）²+2m，在自变量x满足m≤x≤m+2的情况下，与其对应的函数值y的最小值为5，则m的值为（　　）

A . ﹣2或2 B . ﹣2或 $\text{[math]}$ C . 2或 $\text{[math]}$ D . ﹣2或2或 $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019九上·西城期中) 已知函数 $\text{[math]}$ ，则使y=k成立的x值恰好有三个，则k的值为（）

A . 0 B . 1 C . 2 D . 3

答案解析收藏纠错 + 选题
6. (2021九上·舟山期末) 点P（x₁ ， y₁），Q（x₂ ， y₂）在抛物线y＝ax²-4ax＋2（a＞0）上，若对于t＜x₁＜t＋1，t＋2＜x₂＜t＋3，都有y₁≠y₂ ，则t的取值范围是（）

A . t≥1 B . t≤0 C . t≥1或t≤0 D . t≥1或t≤-1

答案解析收藏纠错 + 选题
7. (2021九上·烟台期中) 如图，抛物线 $\text{[math]}$ 过点 $\text{[math]}$ ，且对称轴为直线 $\text{[math]}$ ，有下列结论① $\text{[math]}$ ；② $\text{[math]}$ ：③抛物线经过点 $\text{[math]}$ 与点 $\text{[math]}$ ，则 $\text{[math]}$ ；④无论a，b，c取何值，抛物线都经过同一个点 $\text{[math]}$ ；⑤ $\text{[math]}$ ，其中正确的结论是（）

A . ①②③ B . ③④⑤ C . ②③④ D . ②④⑤

答案解析收藏纠错 + 选题
8. (2021九上·上思期中) 如图所示，已知二次函数y=ax²+bx+c的图象与x轴交于A、B两点，与y轴交于点C对称轴为直线x=1.直线y=﹣x+c与抛物线y=ax²+bx+c交于C、D两点，D点在x轴下方且横坐标小于3，则下列结论：
①2a+b+c＞0；②a﹣b+c＜0；③x（ax+b）≤a+b；④a＜﹣1.

其中正确的有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
9. (2021九上·瑶海月考) 如图，是二次函数y=ax²+bx+c（a≠0）的图象的一部分，给出下列命题：
①abc＜0；②b＞2a；③a+b+c=0；④8a+c＞0；⑤ax²+bx+c=0的两根分别为﹣3和1．

其中正确的命题有（）

A . 2个 B . 3个 C . 4个 D . 5个

答案解析收藏纠错 + 选题
10. (2021九上·梁溪期末) 已知当 $\text{[math]}$ 时，二次函数 $\text{[math]}$ 的值恒大于1，则k的取值范围是（）

A . k≥ $\text{[math]}$ B . － $\text{[math]}$ ≤k≤－ $\text{[math]}$ C . － $\text{[math]}$ ＜k＜0 D . － $\text{[math]}$ ≤k＜0

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·海淀期中) 已知 $\text{[math]}$ ， $\text{[math]}$ 为抛物线 $\text{[math]}$ （ $\text{[math]}$ ）上任意两点，其中 $\text{[math]}$ ．若对于 $\text{[math]}$ ，都有 $\text{[math]}$ ，则a的取值范围是．

答案解析收藏纠错 + 选题
12. (2020九上·海珠期中) 已知函数y＝ $\text{[math]}$ ，且使y＝k成立的x值恰好有2个，则k的取值范是．

答案解析收藏纠错 + 选题
13. (2019九上·朝阳期末) 如图，在平面直角坐标系中，抛物线 $\text{[math]}$ 的顶点为A ，与x轴分别交于O、B两点．过顶点A分别作AC⊥x轴于点C ， AD⊥y轴于点D ，连结BD ，交AC于点E ，则△ADE与△BCE的面积和为．

答案解析收藏纠错 + 选题
14. (2022九上·慈溪期中) 如图，在平面直角坐标系xOy中，抛物线y＝-x²+6x+c的对称轴与x轴交于点A，在直线AB：y＝kx+3上取一点B，使点B在第四象限，且到两坐标轴的距离和为7，设P是抛物线的对称轴上的一点，点Q在抛物线上，若以点A，B，P，Q为顶点的四边形为正方形，则c的值为．

答案解析收藏纠错 + 选题
15. (2022九上·福州开学考) 如图，正方形ABCD的边长为2，E为边AD上一动点，连接CE，以CE为边向右侧作正方形CEFG，连接DF，DG，则 $\text{[math]}$ 面积的最小值为．

答案解析收藏纠错 + 选题

三、解答题

16. 在平面直角坐标系中，点 $\text{[math]}$ ，点 $\text{[math]}$ .已知抛物线 $\text{[math]}$ （ $\text{[math]}$ 是常数），顶点为 $\text{[math]}$ .
（Ⅰ）当抛物线经过点 $\text{[math]}$ 时，求顶点 $\text{[math]}$ 的坐标；

（Ⅱ）若点 $\text{[math]}$ 在 $\text{[math]}$ 轴下方，当 $\text{[math]}$ 时，求抛物线的解析式；

（Ⅲ）无论 $\text{[math]}$ 取何值，该抛物线都经过定点 $\text{[math]}$ .当 $\text{[math]}$ 时，求抛物线的解析式.

答案解析收藏纠错 + 选题
17. (2019九上·如皋期末) 复习课中，教师给出关于x的函数 $\text{[math]}$ （k是实数）.
教师：请独立思考，并把探索发现的与该函数有关的结论（性质）写到黑板上.

学生思考后，黑板上出现了一些结论.教师作为活动一员，又补充一些结论，并从中选择如下四条：

①存在函数，其图像经过（1，0）点；

②函数图象与坐标轴总有三个不同的交点；

③当 $\text{[math]}$ 时，不是y随x的增大而增大就是y随x的增大而减小；

④若函数有最大值，则最大值必为正数，若函数有最小值，则最小值必为负数；

教师：请你分别判断四条结论的真假，并给出理由，最后简单写出解决问题时所用的数学方法.

答案解析收藏纠错 + 选题
18. (2018九上·大庆期中) 二次函数 $\text{[math]}$ 的图象如图所示，根据图象解答下列问题：
1. （1）写出不等式 $\text{[math]}$ 的解集；
2. （2）当 $\text{[math]}$ 时，写出函数值y的取值范围。
3. （3）若方程 $\text{[math]}$ 有两个不相等的正实数根，写出 $\text{[math]}$ 的取值范围。
答案解析收藏纠错 + 选题

四、综合题

19. (2021九上·南部月考) 如图，直线 $\text{[math]}$ 交x轴于A点，交y轴于B点，过A、B两点的抛物线的顶点坐标(1，4)．
1. （1）求k的值和抛物线的解析式；
2. （2）在抛物线的对称轴上求一点P ，使得 $\text{[math]}$ PAB的周长最小，并求出最小值；
3. （3）在抛物线的对称轴上是否存在点Q ，使 $\text{[math]}$ ABQ是等腰三角形？若存在，求出符合条件的Q点坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题
20. 已知二次函数图象的顶点为（3，﹣1），与y轴交于点（0，﹣4）．
1. （1）求二次函数解析式；
2. （2）求函数值y＞﹣4时，自变量x的取值范围．
答案解析收藏纠错 + 选题
21. (2022九上·温州月考) 在平面直角坐标系中，二次函数 $\text{[math]}$ （ $\text{[math]}$ ， m为常数）的图象记作G，图象G上点A的横坐标为2m．
1. （1）当 $\text{[math]}$ ，求图象G的最低点坐标；
2. （2）平面内有点 $\text{[math]}$ ．当AC不与坐标轴平行时，以AC为对角线构造矩形ABCD，AB与x轴平行，BC与y轴平行．
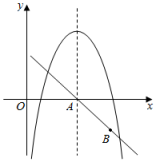
  ①若矩形ABCD为正方形时，求点A坐标；
  ②图象G与矩形ABCD的边有两个公共点时，求m的取值范围．
答案解析收藏纠错 + 选题
22. (2021九上·萧山月考) 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，将点 $\text{[math]}$ 向右平移 $\text{[math]}$ 个单位长度，得到点 $\text{[math]}$ ，点 $\text{[math]}$ 在抛物线上。
1. （1）求点 $\text{[math]}$ 的坐标 $\text{[math]}$ 用含 $\text{[math]}$ 的式子表示 $\text{[math]}$ ；
2. （2）求抛物线的对称轴；
3. （3）已知点P( $\text{[math]}$ ， $\text{[math]}$ )， $\text{[math]}$ ，若抛物线与线段 $\text{[math]}$ 恰有一个公共点，结合函数图象，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题