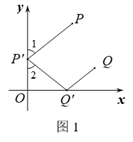
 B .
B .  C .
C .  D .
D . 

![]()
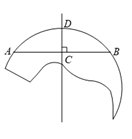
作法:
①分别以A,B为圆心, 长为半径画弧,在直线l下方交于点O;
②以点O为圆心, 长为半径画圆;
③在劣弧 上任取一点C(不与A,B重合),连接
,
.
就是所求作的三角形.
证明:在优弧 上任取一点M(不与A,B重合),连接
,
,
,
.
∵ ,
∴ 是等边三角形.
∴ .
∵A,B,M在⊙ 上,
∴ ()(填推理的依据).
∴ .
∵四边形 内接于⊙O,
∴ ()(填推理的依据).
∴ .
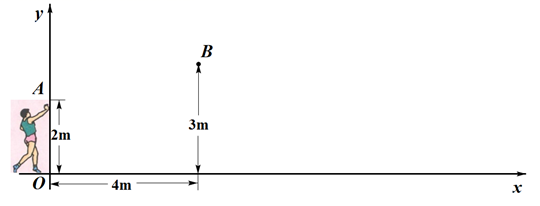
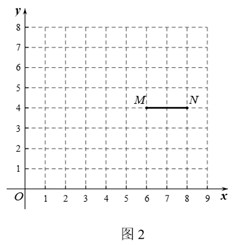
①若 ,求抛物线的表达式;
②若 ,结合函数图象,直接写出N的取值范围.
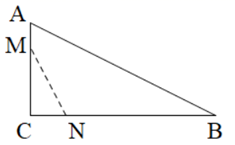
②求证: =
+
;