| x | 1.98 | 1.99 | 2.00 | 2.01 |
| | -0.06 | -0.05 | -0.03 | 0.01 |
判断方程 (
,a,b,c为常数)一个根x的范围是( )

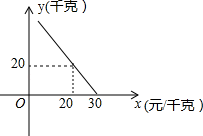
 B .
B .  C .
C .  D .
D . 
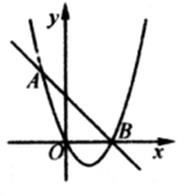

乒乓球到球台的竖直高度记为(单位:
),乒乓球运行的水平距离记为
(单位:
).测得如下数据:
|
水平距离x/ |
|
|
|
|
|
|
|
|
竖直高度y/ |
|
|
|
|
|
|
|

②求满足条件的抛物线解析式;
我们通过下列步骤估计方程2x2+x﹣2=0的根的所在的范围.
第一步:画出函数y=2x2+x﹣2的图象,发现图象是一条连续不断的曲线,且与x轴的一个交点的横坐标在0,1之间.
第二步:因为当x=0时,y=﹣2<0;当x=1时,y=1>0.
所以可确定方程2x2+x﹣2=0的一个根x1所在的范围是0<x1<1.
第三步:通过取0和1的平均数缩小x1所在的范围;
取x= ,因为当x=
时,y<0,
又因为当x=1时,y>0,
所以 <x1<1.
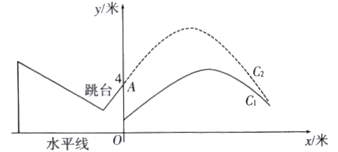

①此抛物线的函数表达式为 ▲ . (函数表达式用一般式表示)
②按规定,车顶部与隧道顶部在竖直方向上的高度差至少0.5米,则此隧道限高 ▲ 米.
③已知人行道台阶高均为0.3米,按照国家标准,人行道宽度不得低于1.25米,该隧道的人行道宽度设计是否达标?说明理由.
+

x(场) | 3 | 10 | 25 |
p(万元) | 10.6 | 12 | 14.2 |