黑龙江省哈尔滨市南岗区松雷中学2023-2024学年七年级上...

更新时间：2023-10-29 浏览次数：34 类型：开学考试

一、选择题（每小题3分，共计24分）

1. (2023七上·南岗开学考) 下列方程中，是一元一次方程的是（）

A . x²＋2x＝3 B . $\text{[math]}$ C . 4x＋y＝1 D . 3x－5＝3

答案解析收藏纠错 + 选题
2. (2023七上·南岗开学考) 为了考察某市初中3500名毕业生的数学成绩，从中抽出20本试卷，每本30份，在这个问题中，样本容量是（）

A . 3500 B . 20 C . 30 D . 600

答案解析收藏纠错 + 选题
3. (2023七上·南岗开学考) 下列变形中正确的是（）

A . 若x＋3＝5－3x ， x＋3x＝5＋3 B . 若m＝n ，则am＝an C . 若a＝b ，则a＋c＝b－c D . 若x＝y ，则 $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023七上·南岗开学考) 下面四个图形中， $\text{[math]}$ 与 $\text{[math]}$ 是同位角的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023七上·南岗开学考) 把方程 $\text{[math]}$ 去分母后，正确的结果是（）

A . 2x－1＝1－（3－x） B . 2（2x－1）＝1－（3－x） C . 2（2x－1）＝8－3－x D . 2（2x－1）＝8－（3－x）

答案解析收藏纠错 + 选题
6. (2023七上·南岗开学考) 某车间有22名工人，每人每天可以生产1200个螺钉或2000个螺母，1个螺钉需要配2个螺母，为使每天生产的螺钉和螺母刚好配套，设有x名工人生产螺钉，其他工人生产螺母，根据题意所列方程正确的是（）

A . 2×1200x＝2000（22－x） B . 2000x＝12000（22－x） C . 2×2000x＝1200（22－x） D . 1200x＝2000（22－x）

答案解析收藏纠错 + 选题
7. (2023七上·南岗开学考) 有理数a ， b在数轴上的位置如图所示，则下列选项正确的是（）

A . |a|＞|b| B . ab＞0 C . a＋b＞0 D . |a－b|＞1

答案解析收藏纠错 + 选题
8. (2023七上·南岗开学考) 下列说法中错误的有（）个．
①多项式3x²-2x＋1的一次项系数是2；②单项式 $\text{[math]}$ 的系数是－2；③单项式和多项式统称为整式；④若 $\text{[math]}$ 与 $\text{[math]}$ 是同类项，那么m－n＝－1

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题

二、填空题（每小题3分，共计24分）

9. (2023七上·乌鲁木齐月考) 新疆的总面积约为1660000平方公里，是中国面积最大的省区，约占我国国土面积的六分之一，1660000用科学记数法可表示为．

答案解析收藏纠错 + 选题
10. (2023七上·南岗开学考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
11. (2024七上·丰满月考) 用四舍五入法把0.0568精确到千分位为．

答案解析收藏纠错 + 选题
12. (2023七上·南岗开学考) 若∠1的对顶角是∠2，∠2的邻补角是∠3，且∠3是54°，则∠1＝．

答案解析收藏纠错 + 选题
13. (2023七上·南岗开学考) 若 $\text{[math]}$ 与 $\text{[math]}$ 互为相反数，则a的值为．

答案解析收藏纠错 + 选题
14. (2023七上·南岗开学考) 某班级原来女生人数是全班人数的 $\text{[math]}$ ，调入4名女生后，女生人数是全班人数的一半，原来全班共有人．

答案解析收藏纠错 + 选题
15. (2023七上·南岗开学考) 如图，直线AB和CD相交于O ， OA平分∠COE ， ∠COE∶∠BOE＝2∶5，则∠EOD的度数为．

答案解析收藏纠错 + 选题
16. (2023七上·南岗开学考) 直线AB上有两点C、D ，点C在A、B之间，满足 $\text{[math]}$ ，若AB＝20，则BD＝．

答案解析收藏纠错 + 选题

三、解答题（其中17－18题各6分，19－23题各8分，24－25题各10分，共计72分）

17. (2023七上·南岗开学考) 计算
1. （1）－5²＋（－7）×（－9）－16＋（－2）³
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2023七上·南岗开学考) 解方程
1. （1） 1－3（8－x）＝－2（15－2x）
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2024七上·大祥期末) 先化简，再求值：
$\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2023七上·南岗开学考) 如图所示，已知∠1＋∠2＝180°，∠3＝∠B ，求证：∠AED＝∠C ．请在括号里填上推理依据．

证明：∵∠1＋∠2＝180°（已知）

∠1＋∠4＝180°（）

∴∠2＝∠4．（）

∴AB∥EG（）

∴∠3＝ ▲ ，

又∵∠3＝∠B（已知）

∴∠ ▲ ＝∠ ▲ （）

∴DE∥BC

∴∠AED＝∠C ．（）

答案解析收藏纠错 + 选题

21. (2023七上·南岗开学考) 中华文明，源远流长：中华汉字，寓意深广．为了传承优秀传统文化，某校团委组织了一次全校2000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分，为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：

成绩/分	频数	频率
50≤x＜60	10	0.05
60≤x＜70	20	0.10
70≤x＜80	30	b
80≤x＜90	a	0.30
90≤x≤100	80	0.40

请根据所给信息，解答下列问题：

（1） a＝，b＝；
（2）通过计算补全频数分布直方图；
（3）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的2000名学生中成绩“优”等的大约有多少人？

答案解析收藏纠错 + 选题

22. (2023七上·南岗开学考) 已知：点D在线段AB上，点C是线段AD的中点，AB=4。
1. （1）如图1，点D是线段AB的中点，求线段CD的长度；
2. （2）如图2，点E是线段BD的中点，求线段CE的长度。
答案解析收藏纠错 + 选题
23. (2023七上·南岗开学考) 某商场分别购进了甲、乙两种型号扫地机器人40台与20台，已知甲种型号扫地机器人的进价比乙种型号扫地机器人的进价便宜10%，甲种型号扫地机器人售价1100元，乙种型号扫地机器人售价1500元。
1. （1） “十一”期间商场促销，乙种型号扫地机器人按售价八折出售，甲种型号扫地机器人按原价销售，某公司一共花了10300元买了9台甲、乙两种型号扫地机器人。问某公司甲、乙两种型号扫地机器人各买了多少台？
2. （2）在（1）的条件下，甲、乙两种型号扫地机器人销售一空，甲种型号扫地机器人利润是乙种型号扫地机器人利润的2倍。问甲、乙两种型号扫地机器人进价各是多少元？
答案解析收藏纠错 + 选题
24. (2023七上·南岗开学考) 阅读下列材料，并解决相应问题
观察下面一列数：
1，2，4，8，……
我们发现，这一列数从第2项起，每一项与它前一项的比都等于2．
一般地，如果一列数从第2项起，每一项与它前一项的比都等于同一个常数，这一列数就叫做等比数列，这个常数叫做等比数列的公比．
1. （1）如果一个等比数列的第2项是12，第3项是18，则这个等比数列的第1项是，第4项是．
2. （2）为了求等比数列1，2，4，8，……的前2024项的和，可以用如下的方法：
  求此等比数列前2024项的和，即为求 $\text{[math]}$ 的值，可令 $\text{[math]}$ ，则 $\text{[math]}$ ，因此 $\text{[math]}$ ，所以 $\text{[math]}$ ，请仿照以上材料，求出 $\text{[math]}$ 的值，并写明求解过程．
答案解析收藏纠错 + 选题
25. (2023七上·南岗开学考) 如图1，O是直线AB上的一点，OC⊥OD ， OE平分∠BOC ．
1. （1）若∠AOD＝35°，求∠BOE的度数；
2. （2）将图1中的∠DOC绕顶点O顺时针旋转至图2的位置．
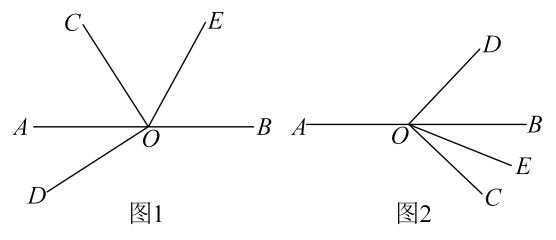
  ①探究∠AOC和∠DOE的度数之间的关系，并说明理由；
  ②在∠AOC的内部有一条射线OF ， ∠BOE内部有一条射线OM ，且3∠AOD－∠AOF＋2∠MOE＝13∠COE＋∠AOF ，试确定∠FOM与∠DOE的度数之间的关系，并说明理由．
答案解析收藏纠错 + 选题