①两点之间,直线最短; ②若AC=BC,则点C是线段AB的中点;③过一点有且只有一条直线与已知直线垂直; ④过一点有且只有一条直线与已知直线平行.其中正确的说法有( )



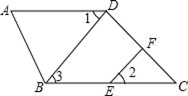
因为∠1=∠2,所以AD∥BC( ).
因为∠A+∠ABC=180°,所以AD∥BC( ).
因为( )∥( ),所以∠C+∠ABC=180°(两直线平行,同旁内角互补)
因为( )∥( ),所以∠3=∠C(两直线平行,同位角相等).
阅读下面的解答过程,并填空(理由或数学式)
解:∵BE∥GF(已知)
∴∠2=∠3.
∵∠1=∠3.
∴∠1=,.
∴DE∥,.
∴∠EDB+∠DBC=180°.
∴∠EDB=180°﹣∠DBC(等式性质)
∵∠DBC=.(已知)
∴∠EDB=180°﹣70°=110°

证明:∵DE∥AB(已知),
∴∠A=∠CED
又∵∠BFD=∠CED(已知),
∴∠A=∠BFD
∴DF∥AE
∴∠EGF+∠AEG=180°

已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵AB∥CD(已知)
∴∠4=∠,.
∵∠3=∠4(已知)
∴∠3=∠,.
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF
即:∠=∠.
∴∠3=∠ .
∴AD∥BE.