云南省昆明市盘龙区2022-2023学年八年级下学期期末数学...

更新时间：2023-10-10 浏览次数：68 类型：期末考试

一、选择题（本大题共12小题，共36.0分。在每小题列出的选项中，选出符合题目的一项）

1. (2023九上·北京市开学考) 下列二次根式中，最简二次根式是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023八下·良庆期末) 下列计算中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023八下·盘龙期末) 如图，四边形 $\text{[math]}$ 中，对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ，下列条件不能判定这个四边形是平行四边形的是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2023八下·盘龙期末) 若二次根式 $\text{[math]}$ 有意义，则 $\text{[math]}$ 的取值范围在数轴上表示为（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023八下·盘龙期末) 如图，直线 $\text{[math]}$ 与x轴交点的横坐标为1，则关于x的方程 $\text{[math]}$ 的解为（）.

A . 1 B . $\text{[math]}$ C . 2 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024八下·昆明期中) 某校进行广播操比赛，如图是20位评委给某班的评分情况统计图，则该班平均得分（　　）

A . 9 B . 6.67 C . 9.1 D . 6.74

答案解析收藏纠错 + 选题
7. (2023八下·盘龙期末) 图1是第七届国际数学教育大会（ICME）会徽，在其主体图案中选择两个相邻的直角三角形，恰好能组合得到如图 $\text{[math]}$ 所示的四边形 $\text{[math]}$ ．若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 4 D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2023八下·盘龙期末) 观察分析下列数据： $\text{[math]}$ ， $\text{[math]}$ ，根据数据排列的规律得到的第 $\text{[math]}$ 个数据的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2023八下·盘龙期末) 对于一次函数 $\text{[math]}$ 的相关性质，下列描述错误的是（）

A . 函数图象经过第一、二、四象限 B . 图象与y轴的交点坐标为 $\text{[math]}$ C . y随x的增大而减小 D . 图象与坐标轴调成三角形的面积为 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023八下·盘龙期末) 如图，在 $\text{[math]}$ 的两边上分别截取OA、OB，使 $\text{[math]}$ ；分别以点 $\text{[math]}$ 为圆心，OA长为半径作弧，两弧交于点C；连接AC、BC、AB、OC若 $\text{[math]}$ ，四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ．则OC的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
11. (2023八下·盘龙期末) 在物理实验课上，小宋利用滑轮组及相关器材进行实验，他把得到的拉力 $\text{[math]}$ 和所悬挂物体的重力 $\text{[math]}$ 的几组数据用电脑绘制成如图所示的图象 $\text{[math]}$ 不计绳重和摩擦 $\text{[math]}$ ，请你根据图象判断以下结论不正确的是（）

A . 施加的拉力 $\text{[math]}$ 随着物体重力 $\text{[math]}$ 的增加而增大 B . 当拉力 $\text{[math]}$ 时，物体的重力 $\text{[math]}$ C . 当物体的重力 $\text{[math]}$ 时，拉力 $\text{[math]}$ D . 当滑轮组未悬挂物体在空中静止时，所用拉力为 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023八下·盘龙期末) 如图所示，在 $\text{[math]}$ 中，分别取 $\text{[math]}$ 、 $\text{[math]}$ 的中点 $\text{[math]}$ 、 $\text{[math]}$ ，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，将 $\text{[math]}$ 分割后拼接成矩形 $\text{[math]}$ 若 $\text{[math]}$ ， $\text{[math]}$ ，则矩形 $\text{[math]}$ 的面积是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共4小题，共8.0分）

13. (2023八下·盘龙期末) $\text{[math]}$ 的三边长分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，那么 $\text{[math]}$ $\text{[math]}$ 填“是”或“不是” $\text{[math]}$ 直角三角形．

答案解析收藏纠错 + 选题

14. (2023八下·盘龙期末) 如表记录了甲、乙、丙三名学生这学期的射击成绩的平均数和方差：

	甲	乙	丙
平均数	9.23	9.3	9.3
方差	0.23	0.017	0.057

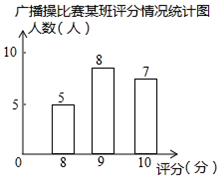
根据表中的数据，要选择一名成绩好且发挥稳定的学生参加比赛，应选择．

答案解析收藏纠错 + 选题

15. (2024八下·石林月考) 将正比例函数 $\text{[math]}$ 向下平移 $\text{[math]}$ 个单位长度，得到一次函数 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
16. (2023·西青模拟) 如图，四边形 $\text{[math]}$ 是正方形，点 $\text{[math]}$ 在 $\text{[math]}$ 边上，点 $\text{[math]}$ 在 $\text{[math]}$ 的延长线上，满足 $\text{[math]}$ ，连接 $\text{[math]}$ 与对角线 $\text{[math]}$ 交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题（本大题共8小题，共56.0分。解答应写出文字说明，证明过程或演算步骤）

17. (2023八下·盘龙期末) 计算：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2023八下·盘龙期末) 已知：如图，四边形 $\text{[math]}$ 是平行四边形， $\text{[math]}$ ，且分别交对角线 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 求证： $\text{[math]}$ ．

答案解析收藏纠错 + 选题

19. (2023八下·盘龙期末) 【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动．

【实践发现】同学们随机收集芒果树、荔枝树的树叶各 $\text{[math]}$ 片，通过测量得到这些树叶的长 $\text{[math]}$ 单位： $\text{[math]}$ ，宽 $\text{[math]}$ 单位： $\text{[math]}$ 的数据后，分别计算长宽比，整理数据如下：

	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
芒果树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
荔枝树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

【实践探究】分析数据如下：

	平均数	中位数	众数	方差
芒果树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
荔枝树叶的长宽比	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

【问题解决】

（1） a= ， $\text{[math]}$ ， $\text{[math]}$ ；
（2） A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大 $\text{[math]}$ ”
$\text{[math]}$ 同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍 $\text{[math]}$ ”以上两位同学的说法中，合理的是同学；
（3）现有一片长 $\text{[math]}$ ，宽 $\text{[math]}$ 的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树？并给出你的理由．

答案解析收藏纠错 + 选题

20. (2023八下·盘龙期末) 在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与直线 $\text{[math]}$ 交于点 $\text{[math]}$ ，点 $\text{[math]}$ 在直线 $\text{[math]}$ 上．
1. （1）求 $\text{[math]}$ 的值；
2. （2）求直线 $\text{[math]}$ 的解析式；
3. （3）直接写出关于 $\text{[math]}$ 的不等式 $\text{[math]}$ 的解集．
答案解析收藏纠错 + 选题
21. (2023八下·盘龙期末) “中国人的饭碗必须牢牢掌握在咱们自己手中” $\text{[math]}$ 为扩大粮食生产规模，某粮食生产基地计划投入一笔资金购进甲、乙两种农机具，已知购进 $\text{[math]}$ 件甲种农机具和 $\text{[math]}$ 件乙种农机具共需 $\text{[math]}$ 万元，购进 $\text{[math]}$ 件甲种农机具和 $\text{[math]}$ 件乙种农机具共需 $\text{[math]}$ 万元．
1. （1）求购进 $\text{[math]}$ 件甲种农机具和 $\text{[math]}$ 件乙种农机具各需多少万元？
2. （2）若该粮食生产基地计划购进甲、乙两种农机具共 $\text{[math]}$ 件，且投入资金不少于 $\text{[math]}$ 万元又不超过 $\text{[math]}$ 万元，设购进甲种农机具 $\text{[math]}$ 件，则有哪几种购买方案？哪种购买方案需要的资金最少，最少资金是多少？
答案解析收藏纠错 + 选题
22. (2023八下·辛集期末) 如图，在平行四边形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC于点E，延长BC到点F，使CF＝BE，连接DF．
1. （1）求证：四边形ADFE是矩形；
2. （2）连接OF，若AD＝6，EC＝4，∠ABF＝60°，求OF的长度．
答案解析收藏纠错 + 选题
23. (2023八下·盘龙期末) 阅读下面的情景对话，然后解答问题：
老师：我们新定义一种三角形，两边平方和等于第三边平方的 $\text{[math]}$ 倍的三角形叫做奇异三角形．
小华：等边三角形一定是奇异三角形 $\text{[math]}$ 并做了如下证明：
设等边三角形的边长为 $\text{[math]}$ ，
$\text{[math]}$ ，
$\text{[math]}$ 等边三角形一定是奇异三角形．
小明：那直角三角形是否存在奇异三角形呢？
1. （1）在 $\text{[math]}$ 中，两直角边长分别是 $\text{[math]}$ 、 $\text{[math]}$ ，这个三角形是否是奇异三角形？请说明理由．
2. （2）在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，若 $\text{[math]}$ 是奇异三角形，求 $\text{[math]}$ ： $\text{[math]}$ ： $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题
24. (2023八下·盘龙期末) 如图，在平面直角坐标系中，直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，过点 $\text{[math]}$ 的直线交 $\text{[math]}$ 轴正半轴于点 $\text{[math]}$ ，且 $\text{[math]}$ 面积为 $\text{[math]}$ ．
1. （1）求点 $\text{[math]}$ 的坐标及直线 $\text{[math]}$ 的解析式；
2. （2）如图 $\text{[math]}$ ，设点 $\text{[math]}$ 为线段 $\text{[math]}$ 中点，点 $\text{[math]}$ 为 $\text{[math]}$ 轴上一动点，连接 $\text{[math]}$ ，以 $\text{[math]}$ 为边向 $\text{[math]}$ 右侧作正方形 $\text{[math]}$ ，在 $\text{[math]}$ 点的运动过程中，当顶点 $\text{[math]}$ 落在直线 $\text{[math]}$ 上时，求点 $\text{[math]}$ 的坐标．
答案解析收藏纠错 + 选题