


 B .
B . 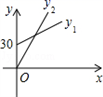 C .
C . 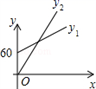 D .
D . 
 B .
B . 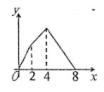 C .
C . 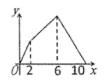 D .
D . 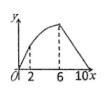

|
型号 |
A |
B |
|
单个盒子容量(升) |
2 |
3 |
|
单价(元) |
5 |
6 |


|
|
1 |
2 |
3 |
4 |
5 |
|
|
3.6 |
5.2 |
6.8 |
8.4 |
10 |


每箱运费(元/每箱) | ||
甲仓库 | 乙仓库 | |
老百姓药房 | 5 | 3.5 |
江南药房 | 4.8 | 3.2 |
每箱运费(元/每箱) | ||
甲仓库 | 乙仓库 | |
老百姓药房 | x | () |
江南药房 | () | |

①求y关于x的关系式;
②进货时,A类图书的购进数量不少于60本,已知A类图书每本的售价为38元,B类图书每本的售价为50元,求如何进货才能使书店所获利润最大,最大利润为多少元?
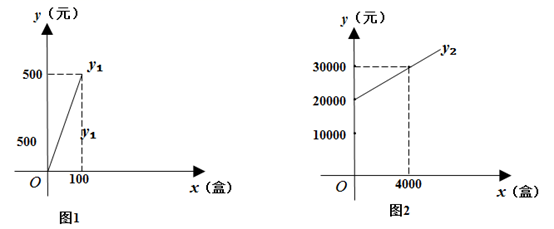
方案一:从包装盒加工厂直接购买,购买所需的费 与包装盒数
满足如图1所示的函数关系.
方案二:租赁机器自己加工,所需费用 (包括租赁机器的费用和生产包装盒的费用)与包装盒数x满足如图2所示的函数关系.根据图象回答下列问题:

【初步探究】