一、单项选择题(本大题共6小题,每小题3分,共18分)
-
1.
(2023八上·南昌期中)
第19届亚运会于2023年9月23日至10月8日在杭州举办,下列关于体育运动的图标中,是轴对称图形的是( )
-
-
A . 内角和、外角和均增加 B . 外角和不变,内角和增加
B . 外角和不变,内角和增加 C . 内角和不变,外角和增加
C . 内角和不变,外角和增加 D . 内角和、外角和均不变
D . 内角和、外角和均不变
-
-
A . -7
B . -1
C . 1
D . 7
-
6.
(2023八上·南昌期中)
两个底角为

、顶角为

的等腰三角形,叫做“黄金三角形”,这种三角形既美观又标准.如图,在

中,

,

,
BD ,
CE为

的角平分线,则图中“黄金三角形”的个数是( )

A . 1
B . 4
C . 5
D . 6
二、填空题(本大题共6小题,每小题3分,共18分)
-
-
-
-
-
-
12.
(2023八上·南昌期中)
在平面直角坐标系中,点

, 点

, 点

, 若

是以
OA为直角边的等腰直角三角形,则点
B的坐标为
.
三、解答题(本大题共5小题,每小题6分,共30分)
-
-
(1)
如图,若正方形和正八边形的一边重合,求

的度数.

-
-
-
-
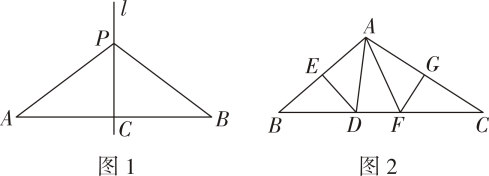
(1)
小贤露营时带着如图1所示的折叠凳,打开时坐着舒适、稳定.这种设计所运用的数学原理是.
-
(2)
图2是折叠凳打开后的侧面示意图,凳腿
AB和
CD的长度相等,交点
O是
AB ,
CD的中点.经过实验,厂家将打开后的折叠凳的宽度
AD设计为

, 求此时
BC的宽度,并说明理由.
-
16.
(2023八上·南昌期中)
如图,请仅用无刻度直尺完成以下作图(保留作图痕迹).

⑴在图1中作 , 使得
, 使得 与
与 关于x轴对称.
关于x轴对称.
⑵在图2中作AB边上的高CD.
-
-
(1)
定理证明
为了证明该性质,珍珍画出了图形,并写出了“已知”和“求证”,请你完成证明过程.
已知:如图1,直线 , 垂足为C ,
, 垂足为C ,  , 点P在直线l上,求证:
, 点P在直线l上,求证: .
.
-
四、解答题(本大题共3小题,每小题8分,共24分)
-
-
(1)
连接AD , 写出线段AD与直线l的关系.
-
(2)
求

的度数.
-
(3)
求

的周长和

的面积.
-
19.
(2023八上·南昌期中)
如图,在正六边形
ABCDEF中,
M ,
N分别是边
BC ,
CD上的点,且

,
AM与
BN交于点
Q.

-
(1)
求证:

;
-
(2)
求

的度数.
-
20.
(2023八上·南昌期中)
如图,在四边形
ABCD中,

, 连接对角线
AC ,
E为
CD的中点,连接
AE并延长,交
BC的延长线于点
F ,
AF平分

.

-
(1)
求证:

.
-
五、解答题(本大题共2小题,每小题9分,共18分)
-
-
(1)
证明:

是直角三角形.
-
(2)
如图2,若
AE是角平分线,
AE与
CD相交于点
F.请判断

是否为等腰三角形,并说明理由.
-
22.
(2023八上·南昌期中)
阅读信息:如图1,在

中,

,

,
D是

外一点,且

, 求

的度数.
图1

图2

解:设

.
∵

是等腰三角形,∴

.
又∵

, ∴

, ∴

.
同理,∵

是等腰三角形,∴

,
∴

.
请根据阅读信息解决问题.
如图2,在

中,

,

,
D是

外一点,且

, 求

的度数.
六、解答题(本大题共12分)
-
23.
(2023八上·南昌期中)
综合与实践
问题提出
如图1,在 中,AD平分
中,AD平分 , 交BC于点D , 且
, 交BC于点D , 且 , 则AB , CD , AC之间存在怎样的数量关系?并说明理由.
, 则AB , CD , AC之间存在怎样的数量关系?并说明理由.

-
(1)
方法运用
我们可以通过作辅助线,构造全等三角形来解题.如图2,延长AC至点E , 使得 , 连接DE , ……,请判断AB , CD , AC之间的数量关系并补充完整解题过程.
, 连接DE , ……,请判断AB , CD , AC之间的数量关系并补充完整解题过程.
-
(2)
以上方法叫做“补短法”.我们还可以采用“截长法”,即通过在
AB上截取线段构造全等三角形来解题.如图3,在线段
AB上截取
AF , 使得

①
▲ , 连接②
▲ .请补全空格,并在图3中画出辅助线.
-
 B .
B .  C .
C .  D .
D . 



,
,
, …是l上的点,分别量一量点
,
,
, …到点A与点B的距离,你有什么发现?可以发现,点
,
,
, …到点A的距离与它们到点B的距离分别相等.
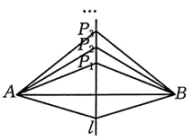
, 垂足为C ,
, 点P在直线l上,求证:
.
中,
, DE , FG分别是边AB , AC的垂直平分线,与
的交点分别为D , E , F , G , 连接AD , AF , 求
的周长.
 图2
图2
, 连接DE , ……,请判断AB , CD , AC之间的数量关系并补充完整解题过程.
,
,
, 若
, 求
的度数.