
 B .
B .  D .
D . 
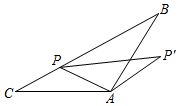






【学习研究】:北师大版教材九年级上册第39页介绍了我国数学家赵爽在其所著的《勾股圆方图注》中关于一元二次方程的几何解法:以为例,构造方法如下:
首先将方程变形为
, 然后画四个长为
, 宽为
的矩形,按如图(1)所示的方式拼成一个“空心”大正方形,则图中大正方形的面积可表示为
, 还可表示为四个矩形与一个边长为2的小正方形面积之和,即
, 因此,可得新方程:
,
表示边长,
, 即
, 遗憾的是,这样的做法只能得到方程的其中一个正根.

【类比迁移】:小明根据赵爽的办法解方程 , 请你帮忙画出相应的图形,将其解答过程补充完整:
第一步:将原方程变形为 , 即
( ▲ )=4;
第二步:利用四个面积可用表示为 ▲ 的全等矩形构造“空心”大正方形(请在画图区画出示意图,标明各边长),并写出完整的解答过程;
第三步:
【拓展应用】:一般地对于形如:一元二次方程可以构造图2来解,已知图2是由4个面积为3的相同矩形构成,中间围成的正方形面积为4.那么此方程的系数
▲ ,
▲ , 求得方程的一个正根为 ▲ .