广东省东莞市重点中学2023-2024学年高二上学期12月月...

更新时间：2024-01-17 浏览次数：25 类型：月考试卷

一、单选题：（本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2023高二上·东莞月考) 直线 $\text{[math]}$ 的倾斜角为（）

A . 60° B . 120° C . 150° D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023高二上·东莞月考) 已知 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 6 D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023高二上·东莞月考) 下列叙述正确的是（）

A . 数列 $\text{[math]}$ 是递增数列 B . 数列0，1，2，3，…的一个通项公式为 $\text{[math]}$ C . 数列0，0，0，1，…是常数列 D . 数列2，4，6，8与数列8，6，4，2是相同的数列

答案解析收藏纠错 + 选题
4. (2023高二上·东莞月考) 已知直线 $\text{[math]}$ 与 $\text{[math]}$ 垂直，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
5. (2023高二上·东莞月考) 设 $\text{[math]}$ 、 $\text{[math]}$ 是两条不同的直线， $\text{[math]}$ 、 $\text{[math]}$ 是两个不同的平面，则能得出 $\text{[math]}$ 的是（）

A . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2023高二上·东莞月考) 已知椭圆 $\text{[math]}$ 的左、右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 在椭圆 $\text{[math]}$ 上，则 $\text{[math]}$ 的内切圆半径的取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2023高二上·东莞月考) 设抛物线 $\text{[math]}$ ，直线 $\text{[math]}$ 与抛物线交于 $\text{[math]}$ 、 $\text{[math]}$ 两点且 $\text{[math]}$ ，则 $\text{[math]}$ 的中点到 $\text{[math]}$ 轴的最短距离为（）

A . $\text{[math]}$ B . 1 C . $\text{[math]}$ D . 2

答案解析收藏纠错 + 选题
8. (2023高二上·东莞月考) 下列数列 $\text{[math]}$ 中，其前 $\text{[math]}$ 项和可能为1028的数列是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多选题：（本题共4小题，每小题满分5分，共20分.在每小题给出的四个选项中，有多项符合题目要求.全部选对得5分，部分选对得2分，有选错的得0分）

9. (2023高二上·东莞月考) 已知双曲线 $\text{[math]}$ ，下列对双曲线 $\text{[math]}$ 判断正确的是（）

A . 实轴长是虚轴长的2倍 B . 焦距为4 C . 离心率为 $\text{[math]}$ D . 渐近线方程为 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2023高二上·东莞月考) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ，下列说法正确的是（）

A . 若点 $\text{[math]}$ 在函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ 为常数）的图象上，则 $\text{[math]}$ 为等差数列 B . 若 $\text{[math]}$ 为等差数列，则 $\text{[math]}$ 为等比数列 C . 若 $\text{[math]}$ 为等差数列， $\text{[math]}$ ， $\text{[math]}$ ，则当 $\text{[math]}$ 时， $\text{[math]}$ 最大 D . 若 $\text{[math]}$ ，则 $\text{[math]}$ 为等差数列

答案解析收藏纠错 + 选题
11. (2023高二上·东莞月考) 已知圆 $\text{[math]}$ ，过点 $\text{[math]}$ 作圆 $\text{[math]}$ 的两条切线，切点分别为 $\text{[math]}$ 、 $\text{[math]}$ ，且直线 $\text{[math]}$ 恒过定点 $\text{[math]}$ ，则（）

A . 点 $\text{[math]}$ 的轨迹方程为 $\text{[math]}$ B . $\text{[math]}$ 的最小值为 $\text{[math]}$ C . 圆 $\text{[math]}$ 上的点到直线 $\text{[math]}$ 的距离的最大值为 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2023高二上·东莞月考) 如图（1）是一副直角三角板.现将两个三角板沿它们的公共边翻折成图（2）的四面体 $\text{[math]}$ ，设 $\text{[math]}$ ， $\text{[math]}$ 与面 $\text{[math]}$ 所成角分别为 $\text{[math]}$ ， $\text{[math]}$ ，在翻折的过程中，下列叙述正确的是（）

A . 若 $\text{[math]}$ ，当 $\text{[math]}$ 时，点 $\text{[math]}$ 到面 $\text{[math]}$ 的距离是2 B . 存在某个位置使得 $\text{[math]}$ C . 若 $\text{[math]}$ ，当二面角 $\text{[math]}$ 时，则 $\text{[math]}$ D . 当 $\text{[math]}$ 在面 $\text{[math]}$ 的射影在三角形 $\text{[math]}$ 的内部（不含边界），则 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：（本题共4小题，每小题5分，共20分）

13. (2023高二上·东莞月考) 已知方程 $\text{[math]}$ 表示焦点在 $\text{[math]}$ 轴上的椭圆，则实数 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
14. (2023高二上·东莞月考) 假设小明每次用相同体积的清水清洗碗筷，且每次能洗去污垢的 $\text{[math]}$ ，那么至少要清洗次才能使存留的污垢在1%以下.

答案解析收藏纠错 + 选题
15. (2023高二上·东莞月考) 如图，四棱锥 $\text{[math]}$ 中，平面 $\text{[math]}$ 平面 $\text{[math]}$ ，底面 $\text{[math]}$ 是边长为2的正方形， $\text{[math]}$ 是等腰三角形，则平面 $\text{[math]}$ 上任意一点到底面 $\text{[math]}$ 中心距离的最小值为.

答案解析收藏纠错 + 选题
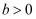
16. (2023高二上·东莞月考) 如图：过双曲线 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的右焦点 $\text{[math]}$ 作直线 $\text{[math]}$ ，且直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 的一条渐近线垂直，垂足为 $\text{[math]}$ ，直线 $\text{[math]}$ 与另一条渐近线交于点 $\text{[math]}$ （ $\text{[math]}$ 、 $\text{[math]}$ 均在 $\text{[math]}$ 轴右侧）.已知 $\text{[math]}$ 为坐标原点，若 $\text{[math]}$ 的内切圆的半径为 $\text{[math]}$ ，则双曲线 $\text{[math]}$ 的离心率为.

答案解析收藏纠错 + 选题

四、解答题：（本题共6小题，共70分.17题10分，18~22题每题12分，解答应写出文字说明、证明过程或演算步骤）

17. (2023高二上·鸡西期中) 已知直线 $\text{[math]}$ 和圆 $\text{[math]}$ .
1. （1）判断直线 $\text{[math]}$ 与圆 $\text{[math]}$ 的位置关系；若相交，求直线 $\text{[math]}$ 被圆 $\text{[math]}$ 截得的弦长；
2. （2）求过点 $\text{[math]}$ 且与圆 $\text{[math]}$ 相切的直线方程.
答案解析收藏纠错 + 选题
18. (2023高二上·东莞月考) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ .
1. （1）证明： $\text{[math]}$ 是等差数列；
2. （2）设 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .
答案解析收藏纠错 + 选题
19. (2023高二上·东莞月考) 已知椭圆 $\text{[math]}$ ，左右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 与椭圆交于 $\text{[math]}$ ， $\text{[math]}$ 两点，弦 $\text{[math]}$ 被点 $\text{[math]}$ 平分.
1. （1）求直线 $\text{[math]}$ 的方程；
2. （2）求 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
20. (2023高二上·东莞月考) 如图，在斜三棱柱 $\text{[math]}$ 中，已知 $\text{[math]}$ 为正三角形，四边形 $\text{[math]}$ 是菱形， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的中点，平面 $\text{[math]}$ 平面 $\text{[math]}$ .
1. （1）若 $\text{[math]}$ 是线段 $\text{[math]}$ 的中点，求证： $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ 是线段 $\text{[math]}$ 的一点（如图），且 $\text{[math]}$ ，二面角 $\text{[math]}$ 的余弦值为 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
21. (2023高二上·东莞月考) 已知数列 $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ 为数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和， $\text{[math]}$ ，（ $\text{[math]}$ ），记 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ， $\text{[math]}$ 的前 $\text{[math]}$ 项积为 $\text{[math]}$ ，且 $\text{[math]}$ .
1. （1）求数列 $\text{[math]}$ ， $\text{[math]}$ 的通项公式；
2. （2）令 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .
答案解析收藏纠错 + 选题
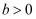
22. (2023高二上·东莞月考) 已知双曲线 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的左，右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ，左顶点为 $\text{[math]}$ ，直线 $\text{[math]}$ 过左焦点 $\text{[math]}$ ，与双曲线 $\text{[math]}$ 的左，右两支依次交于 $\text{[math]}$ ， $\text{[math]}$ 两点.当 $\text{[math]}$ 轴时， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求双曲线 $\text{[math]}$ 的标准方程；
2. （2）点 $\text{[math]}$ 和点 $\text{[math]}$ 关于 $\text{[math]}$ 轴对称（两个点不重合），直线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题