一、选择题(本大题共10小题,每个小题3分,每个小题给出的四个选项中,只有一项是符合题目要求的)
-
-
-
A . 1cm、2cm、3cm
B . 3cm、4cm、8cm
C . 4cm、4cm、9cm
D . 8cm、8cm、9cm
-
-
A . (2,3)
B . (-2,3)
C . (-3,2)
D . (-2,-3)
-
-
A . AC=BD
B . ∠CAB=∠DBA
C . ∠C=∠D
D . BC=AD
-
A . 9
B . 10
C . 11
D . 12
-
9.
(2023八上·越秀期中)
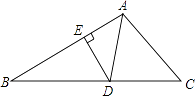
如图,在△ABC中,AD是角平分线,DE⊥AB于点E,△ABC的面积为7,AB=4,DE=2,则AC的长是( )
A . 4
B . 3
C . 6
D . 5
-
10.
(2023八上·越秀期中)
如图,在△
ABC中,
AB=
AC , ∠
BAC=50°,∠
BAC的平分线与
AB的垂直平分线交于点
O , 点
E、
F分别在边
BC、
AC上,点
C沿
EF折叠后与点
O重合,则∠
CEF的度数是( )

A . 60°
B . 55°
C . 50°
D . 45°
二、填空题(本大题共6小题,每小题3分,共18分)
-
-
-
-
-
-
16.
(2023八上·越秀期中)
如图,在△
ABC中,
AB=
AC , ∠
B=∠
C=45°,
D、
E是斜边
BC上两点,且∠
DAE=45°,过点
A作
AF⊥
AD , 垂足是
A , 过点
C作
CF⊥
BC , 垂足是
C . 交
AF于点
F , 连接
EF , 下列结论:①△
ABD≌△
ACF;②
DE=
EF;③若
S△ADE=10,
S△CEF=4,则
S△ABC=24;④
BD+
CE=
DE . 其中正确的是
.

三、解答题(本大题共9小题,共72分,解答题应写出必要的文字说明,推理过程或演算步骤)
-
-
-
-
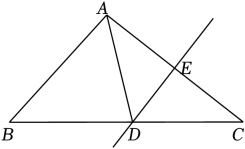
20.
(2023八上·越秀期中)
如图,在△
ABC中,
DE是
AC的垂直平分线,
AC=10,△
ABD的周长为18,求△
ABC的周长.
-
-
-
(2)
若网格上的每个小正方形边长均为1,求

的面积;
-
22.
(2023八上·越秀期中)
如图,△
ABC是等边三角形,延长
BC到
E , 使
CE=
 BC
BC . 点
D是边
AC的中点,连接
ED并延长交
AB于
F .

-
-
-
-
(1)
如图1,判断∠BAD和∠BCD之间的数量关系,并说明理由;
-
(2)
如图2,若∠DAC=60°时,探究线段AB , BC , BD之间的数量关系,并说明理由.
-
-
-
(2)
以A为直角顶点在第二象限内作等腰直角三角形ABE , 过点E作EF⊥x轴于点F , 求点F的坐标;
-
(3)
若点P为y轴正半轴上一动点,以AP为直角边作等腰直角三角形APQ , ∠APQ=90°,QR⊥x轴于点R , 当点P运动时,OP-QR的值是否发生变化?若不变,求出其值;若变化,请说明理由.
-
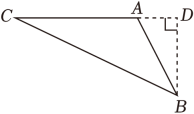
25.
(2023八上·越秀期中)
在△
ABC中,∠
BAC=90°,点
D是
BC边上一点,将△
ACD沿
AD折叠后得到△
AED , 射线
AE交射线
CB于点
F .

-
(1)
当点
D在线段
BC上时,
①如图1,若DE∥AB , 说明AE⊥BC;
②如图2,若DE⊥BC , 请判断∠CAD与∠C的数量关系,并说明理由;
-
(2)
若∠B=2∠C , DE=EF , 求∠CAD的度数.
 B .
B .  C .
C .  D .
D . 
 B .
B .  D .
D .  B .
B .  C .
C . 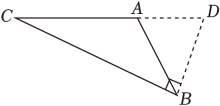 D .
D .