吉林地区普通高中2023-2024学年高三年级上学期数学第一...

更新时间：2024-01-21 浏览次数：37 类型：高考模拟

一、单项选择题：本大题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一个是符合题目要求．

1. (2023·吉林模拟) 已知全集 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023·吉林模拟) 若复数 $\text{[math]}$ ，则 $\text{[math]}$ 的虚部是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2023·吉林模拟) “ $\text{[math]}$ ”是“ $\text{[math]}$ ”的（）

A . 充分不必要条件 B . 必要不充分条件 C . 充要条件 D . 既不充分也不必要条件

答案解析收藏纠错 + 选题
4. (2023·吉林模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·吉林模拟) 在等比数列 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 11

答案解析收藏纠错 + 选题
6. (2023·吉林模拟) 已知函数 $\text{[math]}$ ， $\text{[math]}$ 的定义域均为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 且 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 24 B . 26 C . 28 D . 30

答案解析收藏纠错 + 选题
7. (2023·吉林模拟) 在直角三角形 $\text{[math]}$ 中， $\text{[math]}$ 、 $\text{[math]}$ 的重心、外心、垂心、内心分別为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ （其中 $\text{[math]}$ ），当 $\text{[math]}$ 取最大值时， $\text{[math]}$ （）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
8. (2023·吉林模拟) 已知函数 $\text{[math]}$ 在区间 $\text{[math]}$ 上有且仅有4个极大值点，则正实数 $\text{[math]}$ 的取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题：本大题共4小题，每小题5分，共20分．在每小题给出的四个选项中，有多项符合题目要求．全部选对的得5分，部分选对的得2分，有选错的得0分．

9. (2023·吉林模拟) 已知函数 $\text{[math]}$ （ $\text{[math]}$ ，且 $\text{[math]}$ ）的反函数为 $\text{[math]}$ ，则（）

A . $\text{[math]}$ （ $\text{[math]}$ ，且 $\text{[math]}$ ）且定义域是 $\text{[math]}$ B . 若 $\text{[math]}$ ，则 $\text{[math]}$ C . 函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象关于直线 $\text{[math]}$ 对称 D . 函数 $\text{[math]}$ 与 $\text{[math]}$ 的图象的交点个数可能为0，1，2，3

答案解析收藏纠错 + 选题
10. (2023·吉林模拟) 口袋中装有大小质地完全相同的白球和黑球各2个，从中不放回的依次取出2个球，事件 $\text{[math]}$ “取出的两球同色”，事件 $\text{[math]}$ “第一次取出的是白球”，事件 $\text{[math]}$ “第二次取出的是白球”，事件 $\text{[math]}$ “取出的两球不同色”，则（）

A . $\text{[math]}$ B . $\text{[math]}$ 与 $\text{[math]}$ 互斥 C . $\text{[math]}$ 与 $\text{[math]}$ 相互独立 D . $\text{[math]}$ 与 $\text{[math]}$ 互为对立

答案解析收藏纠错 + 选题
11. (2023·吉林模拟) 等差数列 $\text{[math]}$ 与 $\text{[math]}$ 的前 $\text{[math]}$ 项和分别是 $\text{[math]}$ 与 $\text{[math]}$ ，且 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 的最大值是17 D . $\text{[math]}$ 最小值是7

答案解析收藏纠错 + 选题
12. (2023·吉林模拟) 中华人民共和国国旗是五星红旗，国旗上每个五角星之所以看上去比较美观，是因其图形中隐藏着黄金分割数．连接正五边形的所有对角线能够形成一个标准的正五角星，正五角星中每个等腰三角形都是黄金三角形．黄金三角形分两种：一种是顶角为 $\text{[math]}$ 的等腰三角形，其底边与一腰的长度之比为黄金比 $\text{[math]}$ ；一种是顶角为 $\text{[math]}$ 的等腰三角形，其一腰与底边的长度之比为黄金比 $\text{[math]}$ ．如图，正五角星 $\text{[math]}$ 中， $\text{[math]}$ ，记 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 在 $\text{[math]}$ 上的投影向量为 $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本大题共4小题，每小题5分，共20分．其中第15题的第一个空填对得2分，第二个空填对得3分．

13. (2024高三下·宜宾模拟) 已知 $\text{[math]}$ ，则 $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
14. (2023·吉林模拟) 已知tanθ=2，则sinθcosθ=．

答案解析收藏纠错 + 选题
15. (2023·吉林模拟) 吉林市一中学有男生900人，女生600人．在“书香校园”活动中，为了解全校学生的读书时间，按性别比例分层随机抽样的方法抽取100名学生，其中男生、女生每天读书时间的平均值分别为60分钟和80分钟，方差分别为10和15．结合上述数据估计该校学生每天读书时间的平均值为分钟，方差为．

答案解析收藏纠错 + 选题
16. (2023·吉林模拟) 已知函数 $\text{[math]}$ 若函数 $\text{[math]}$ 有4个零点．则实数 $\text{[math]}$ 的取值范围是．

答案解析收藏纠错 + 选题

四、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．

17. (2023·吉林模拟) 已知向量 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ 且 $\text{[math]}$ ，求 $\text{[math]}$ ；
2. （2）若函数 $\text{[math]}$ ，求 $\text{[math]}$ 的单调递增区间．
答案解析收藏纠错 + 选题
18. (2023·吉林模拟) 已知函数 $\text{[math]}$ ．
1. （1）求曲线 $\text{[math]}$ 在 $\text{[math]}$ 处的切线方程；
2. （2）若对 $\text{[math]}$ ， $\text{[math]}$ 恒成立．求实数 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
19. (2023·吉林模拟) 已知数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）请在①②中选择一个作答，并把序号填在答题卡对应位置的横线上，①求数列 $\text{[math]}$ 的通项公式；②求 $\text{[math]}$ ；
2. （2）令 $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ ，并证明 $\text{[math]}$ ．
答案解析收藏纠错 + 选题
20. (2023·吉林模拟) 近几年以华为为代表的中国高科技企业正在不断突破科技封锁．多项技术已经“遥遥领先”．国产光刻机作为芯片制造的核心设备，也已经取得了突飞猛进的发展．已知一芯片生产商用某国产光刻机生产的 $\text{[math]}$ 型芯片经过十项指标全面检测后，分为Ⅰ级和Ⅱ级，两种芯片的某项指标的频率分布如图所示：
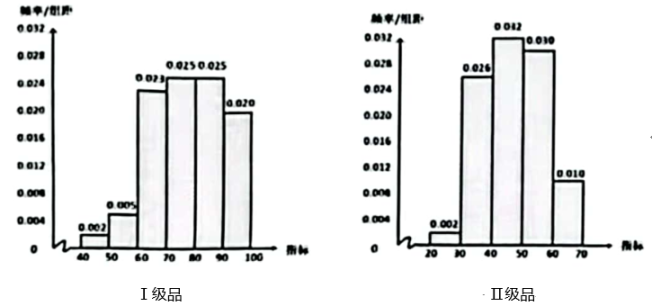
若只利用该指标制定一个标准，需要确定临界值 $\text{[math]}$ ，将该指标大于 $\text{[math]}$ 的产品应用于 $\text{[math]}$ 型手机，小于或等于 $\text{[math]}$ 的产品应用于 $\text{[math]}$ 型手机．假设数据在组内均匀分布，以事件发生的频率作为相应事件发生的概率．
1. （1）求 $\text{[math]}$ 型芯片Ⅰ级品该项指标的第70百分位数；
2. （2）当临界值 $\text{[math]}$ 时，求 $\text{[math]}$ 型芯片Ⅱ级品应用于 $\text{[math]}$ 型手机的概率；
3. （3）已知 $\text{[math]}$ ，现有足够多的 $\text{[math]}$ 型芯片Ⅰ级品、Ⅱ级品，分别应用于 $\text{[math]}$ 型于机、 $\text{[math]}$ 型手机各1万部的生产：
  方案一：直接将 $\text{[math]}$ 型芯片Ⅰ级品应用于 $\text{[math]}$ 型手机，其中该指标小于等于临界值 $\text{[math]}$ 的芯片会导致芯片生产商每部手机损失700元；直接将 $\text{[math]}$ 型芯片Ⅱ级品应用于 $\text{[math]}$ 型手机，其中该指标大于临界值 $\text{[math]}$ 的芯片，会导致芯片生产商每部手机损失300元；
  方案二：重新检测 $\text{[math]}$ 型芯片Ⅰ级品，Ⅱ级品，会避免方案一的损失费用，但检测费用共需要101万元；
  请从芯片生产商的成本考虑，选择合理的方案．
答案解析收藏纠错 + 选题
21. (2023·吉林模拟) 已知 $\text{[math]}$ 的三个角 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的对边分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求角 $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，在 $\text{[math]}$ 的边 $\text{[math]}$ 和 $\text{[math]}$ 上分别取点 $\text{[math]}$ ， $\text{[math]}$ ，将 $\text{[math]}$ 沿线段 $\text{[math]}$ 折叠到平面 $\text{[math]}$ 后，顶点 $\text{[math]}$ 恰好落在边 $\text{[math]}$ 上（设为点 $\text{[math]}$ ），设 $\text{[math]}$ ，当 $\text{[math]}$ 取最小值时，求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
22. (2023·吉林模拟) 已知函数 $\text{[math]}$ ．
1. （1）若函数 $\text{[math]}$ 在 $\text{[math]}$ 上单调递增，求正实数 $\text{[math]}$ 的取值范围；
2. （2）求证：当 $\text{[math]}$ 时， $\text{[math]}$ 在 $\text{[math]}$ 上存在唯一极小值点 $\text{[math]}$ ，且 $\text{[math]}$ ．
答案解析收藏纠错 + 选题