一、单选题(本大题共8小题,共40.0分。在每小题列出的选项中,选出符合题目的一项)
-
-
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
-
-
A . 充分不必要条件
B . 必要不充分条件
C . 充要条件
D . 既不充分也不必要条件
-
5.
(2024·永州模拟)
在平面直角坐标系中,过直线

上一点

作圆

的两条切线,切点分别为

, 则

的最大值为( )
-
6.
(2024·永州模拟)
已知椭圆

的左、右焦点分别是

, 点

是椭圆

上位于第一象限的一点,且

与

轴平行,直线

与

的另一个交点为

, 若

, 则

的离心率为( )
-
-
二、多选题(本大题共4小题,共20.0分。在每小题有多项符合题目要求)
-
A . 两个变量 的相关系数为
的相关系数为 , 则
, 则 越小,
越小, 与
与 之间的相关性越弱
之间的相关性越弱
B . 设随机变量 , 若
, 若 , 则
, 则
C . 在回归分析中, 为
为 的模型比
的模型比 为
为 的模型拟合得更好
的模型拟合得更好
D . 某人解答 个问题,答对题数为
个问题,答对题数为 , 则
, 则
-
-
-
三、填空题(本大题共4小题,共20.0分)
-
13.
(2024·永州模拟)
为全面推进乡村振兴,永州市举办了“村晚兴乡村”活动,晚会有

走,去永州

扬鞭催马运粮忙

数幸福

乡村振兴唱起来

四个节目,若要对这四个节目进行排序,要求

数幸福

与

乡村振兴唱起来

相邻,则不同的排列种数为

用数字作答

.
-
-
-
16.
(2024·永州模拟)
已知点

在抛物线

上,

为抛物线

的焦点,圆

与直线

相交于

两点,与线段

相交于点

, 且

若

是线段

上靠近

的四等分点,则抛物线

的方程为
.
四、解答题(本大题共6小题,共70.0分。解答应写出文字说明,证明过程或演算步骤)
-
-
(1)
求数列

的通项公式;
-
-
-
(1)
求角

;
-
-
19.
(2024·永州模拟)
如图所示,在四棱锥

中,底面

为矩形,侧面

为正三角形,且

分别为

的中点,

在线段

上,且

.
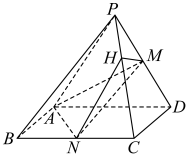
-
(1)
求证:

平面

;
-
-
20.
(2024·永州模拟)
某企业为提高竞争力,成功研发了三种新品

, 其中

能通过行业标准检测的概率分别为

, 且

是否通过行业标准检测相互独立.
-
(1)
设新品

通过行业标准检测的品种数为

, 求

的分布列;
-
(2)
已知新品

中的一件产品经检测认定为优质产品的概率为

, 现从足量的新品

中任意抽取一件进行检测,若取到的不是优质产品,则继续抽取下一件,直至取到优质产品为止,但抽取的总次数不超过

如果抽取次数的期望值不超过

, 求

的最大值.
参考数据:
-
-
(1)
求点

的轨迹

的方程;
-
(2)
设轨迹

与

轴分别交于

两点

在

的左侧

, 过

的直线

与轨迹

交于

两点,直线

与直线

的交于

, 证明:

在定直线上.
-
-
(1)
当

时,求证:

;
-
(2)
若

时,

, 求实数a的取值范围.