安徽省亳州重点中学2023~2024学年高二第一学期全市统考...

更新时间：2024-02-22 浏览次数：40 类型：期末考试

一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项符合题目要求.

1. (2024高二上·亳州期末) 在空间直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ 关于平面 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 10 B . 8 C . 6 D . 4

答案解析收藏纠错 + 选题
2. (2024高二上·亳州期末) 已知三棱锥 $\text{[math]}$ ，点M ， N分别为AB ， OC的中点，且 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，用 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 表示 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2024高二上·亳州期末) 某校有甲、乙等5名同学到4个社区参加志愿服务活动，要求每名同学只能去1个社区，每个社区至少安排1名同学，则甲、乙2人被分配到同一个社区的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024高二上·亳州期末) 手工课可以提高学生的动手能力、反应能力、创造力．某小学生在一次手工课上制作了一座漂亮的房子模型，它可近似地看成是一个直三棱柱和一个正方体的组合体．其直观图如图所示， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 分别是棱 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的中点，则异面直线 $\text{[math]}$ 与 $\text{[math]}$ 所成角的余弦值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高二上·亳州期末) 已知圆 $\text{[math]}$ ： $\text{[math]}$ 与圆 $\text{[math]}$ ： $\text{[math]}$ 相内切，则 $\text{[math]}$ （）

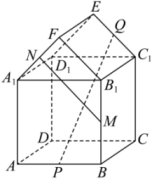
A . 11 B . $\text{[math]}$ C . 9 D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024高二上·亳州期末) 已知两点 $\text{[math]}$ ，若直线 $\text{[math]}$ 与线段 $\text{[math]}$ 有公共点，则直线 $\text{[math]}$ 倾斜角的取值范围为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高二上·亳州期末) 双曲线C： $\text{[math]}$ （ $\text{[math]}$ ）的左顶点为A ，点P ， Q均在C上，且关于y轴对称．若直线AP ， AQ的斜率之积为 $\text{[math]}$ ，则C的渐近线方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高二上·亳州期末) 阅读材料：数轴上，方程 $\text{[math]}$ 可以表示数轴上的点；平面直角坐标系 $\text{[math]}$ 中，
方程 $\text{[math]}$ （ $\text{[math]}$ 、 $\text{[math]}$ 不同时为0）可以表示坐标平面内的直线；空间直角坐标系 $\text{[math]}$ 中，
方程 $\text{[math]}$ （ $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 不同时为0）可以表示坐标空间内的平面．过点 $\text{[math]}$ 且一个法向量为 $\text{[math]}$ 的平面 $\text{[math]}$ 的方程可表示为 $\text{[math]}$ ．阅读上面材料，解决下面问题：已知平面 $\text{[math]}$ 的方程为 $\text{[math]}$ ，直线 $\text{[math]}$ 是两平面 $\text{[math]}$ 与 $\text{[math]}$ 的交线，则直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的正弦值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的选项中，有多项符合题目要求.全部选对的得5分，部分选对的得2分，有选错的得0分.

9. (2024高二上·亳州期末) 已知 $\text{[math]}$ 的展开式共有13项，则下列说法中正确的有（）

A . 所有奇数项的二项式系数和为 $\text{[math]}$ B . 二项式系数最大的项为第7项 C . 所有项的系数和为 $\text{[math]}$ D . 有理项共5项

答案解析收藏纠错 + 选题
10. (2024高二上·亳州期末) 下列四个命题中正确的是（）

A . 已知 $\text{[math]}$ 是空间的一组基底，若 $\text{[math]}$ ，则 $\text{[math]}$ 也是空间的一组基底 B . $\text{[math]}$ 是平面 $\text{[math]}$ 的法向量， $\text{[math]}$ 是直线 $\text{[math]}$ 的方向向量，若 $\text{[math]}$ ，则 $\text{[math]}$ C . 已知向量 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 在 $\text{[math]}$ 方向上的投影向量为 $\text{[math]}$ D . $\text{[math]}$ 为空间中任意一点，若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 四点共面

答案解析收藏纠错 + 选题
11. (2024高二上·保山期中) 已知直线 $\text{[math]}$ 和圆 $\text{[math]}$ ，则（）

A . 直线 $\text{[math]}$ 过定点 $\text{[math]}$ B . 直线 $\text{[math]}$ 与圆 $\text{[math]}$ 有两个交点 C . 存在直线 $\text{[math]}$ 与直线 $\text{[math]}$ 垂直 D . 直线 $\text{[math]}$ 被圆 $\text{[math]}$ 截得的最短弦长为 $\text{[math]}$

答案解析收藏纠错 + 选题
12. (2024高二上·亳州期末) 设椭圆的方程为 $\text{[math]}$ ，斜率为k的直线不经过原点O ，而且与椭圆相交于A ， B两点，M为线段AB的中点，下列结论不正确的是（）

A . 直线AB与OM垂直 B . 若点M坐标为 $\text{[math]}$ ，则直线方程为 $\text{[math]}$ C . 若直线方程为 $\text{[math]}$ ，则点M坐标为 $\text{[math]}$ D . 若直线方程为 $\text{[math]}$ ，则 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分.

13. (2024高二上·亳州期末) 已知向量 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ 与 $\text{[math]}$ 平行，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024高二上·亳州期末) 已知点 $\text{[math]}$ ，圆 $\text{[math]}$ 的半径为1，圆心是直线 $\text{[math]}$ 和直线 $\text{[math]}$ 的交点.若过点 $\text{[math]}$ 的直线 $\text{[math]}$ 与圆 $\text{[math]}$ 有公共点，则直线 $\text{[math]}$ 斜率的取值范围为．

答案解析收藏纠错 + 选题
15. (2024高三上·广州期末) 现有 $\text{[math]}$ 五人排成一列，其中 $\text{[math]}$ 与 $\text{[math]}$ 相邻， $\text{[math]}$ 不排在两边，则共有种不同的排法（用具体数字作答）．

答案解析收藏纠错 + 选题
16. (2024高二上·亳州期末) 在正方体 $\text{[math]}$ 中，设 $\text{[math]}$ ，若二面角 $\text{[math]}$ 的平面角的正弦值为 $\text{[math]}$ ，则实数 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题

四、解答题：本小题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.

17. (2024高二上·亳州期末) 如图，在三棱柱 $\text{[math]}$ 中，所有棱长都为2，且 $\text{[math]}$ ，平面 $\text{[math]}$ 平面 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点，点 $\text{[math]}$ 为 $\text{[math]}$ 的中点．
1. （1）点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离；
2. （2）求点 $\text{[math]}$ 到平面 $\text{[math]}$ 的距离．
答案解析收藏纠错 + 选题
18. (2024高二上·亳州期末) 已知抛物线上的点到焦点F的距离为4．
1. （1）求C的方程；
2. （2）若过点F的直线与C交于不同的两点A ， B ，且 $\text{[math]}$ ，求直线AB的方程．
答案解析收藏纠错 + 选题
19. (2024高二上·亳州期末) 中华文化源远流长，为了让青少年更好地了解中国的传统文化，某培训中心计划利用暑期开设“围棋”、“武术”、“书法”、“剪纸”、“京剧”、“刺绣”六门体验课程．
1. （1）若体验课连续开设六周，每周一门，求“京剧”和“剪纸”课程排在不相邻的两周的所有排法种数；
2. （2）现有甲、乙、丙三名学生报名参加暑期的体验课程，每人都选两门课程，甲和乙有一门共同的课程，丙和甲、乙的课程都不同，求所有选课的种数；
3. （3）计划安排A、B、C、D、E五名教师教这六门课程，每门课程只由一名教师任教，每名教师至少任教一门课程，教师A不任教“围棋”课程，教师B只能任教一门课程，求所有课程安排的种数．
答案解析收藏纠错 + 选题
20. (2024高二上·亳州期末)
1. （1）求 $\text{[math]}$ 除以15的余数；
2. （2）若 $\text{[math]}$ ，求 $\text{[math]}$ 的值；
3. （3）求 $\text{[math]}$ 展开式中系数最大的项．
答案解析收藏纠错 + 选题
21. (2024高二上·亳州期末) 如图，在四棱锥 $\text{[math]}$ 中，底面 $\text{[math]}$ 是菱形， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 平面 $\text{[math]}$ ， $\text{[math]}$ 为线段 $\text{[math]}$ 上的一点．
1. （1）证明：平面 $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）当 $\text{[math]}$ 与平面 $\text{[math]}$ 所成的角的正弦值最大时，求平面 $\text{[math]}$ 与平面 $\text{[math]}$ 夹角的余弦值．
答案解析收藏纠错 + 选题
22. (2024高二上·亳州期末) 已知椭圆 $\text{[math]}$ ，直线 $\text{[math]}$ ，过右焦点 $\text{[math]}$ 的直线(不与 $\text{[math]}$ 轴重合)与椭圆 $\text{[math]}$ 交于 $\text{[math]}$ 两点，过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为 $\text{[math]}$ ．
1. （1）求证：直线 $\text{[math]}$ 过定点 $\text{[math]}$ ，并求出定点 $\text{[math]}$ 的坐标；
2. （2）点 $\text{[math]}$ 为坐标原点，求 $\text{[math]}$ 面积的最大值．
答案解析收藏纠错 + 选题