一、选择题:以下每小题均有A,B,C,D四个选项,其中只有一个选项正确,每小题3分,共36分.
-
-
2.
(2023九上·从江月考)
如图所示,AB∥CD∥EF,AF与BE相交于点G,且AG=2,GD=1,DF=5,则CE∶BC等于( )

A . 5∶3
B . 1∶3
C . 3∶5
D . 2∶3
-
A . 直角三角形都相似
B . 等腰三角形都相似
C . 矩形都相似
D . 等腰直角三角形都相似
-
A . 5
B . 6
C .  D .
D . 
-
5.
(2023九上·从江月考)
如图所示,在△ABC中,D,E分别是AB,AC的中点,若△ADE的面积为4,则△ABC的面积为( )

A . 8
B . 12
C . 14
D . 16
-
6.
(2023九上·从江月考)
如图所示,在平面直角坐标系中,已知点A(-3,6),B(-9,-3),以原点O为位似中心,相似比为

, 把△ABO缩小,则点A的对应点A′的坐标是( )

A . (-1,2)
B . (-9,18)
C . (-9,18)或(9,-18)
D . (-1,2)或(1,-2)
-
7.
(2023九上·从江月考)
矩形相邻的两边长分别为25和

, 把它按如图所示的方式分割成五个全等的小矩形,每一个小矩形均与原矩形相似,则

的值为( )
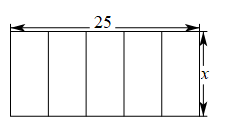
A . 5
B .  C .
C .  D . 10
D . 10
-
8.
(2023九上·从江月考)
如图所示,小红同学正在使用手电筒进行物理光学实验,地面上从左往右依次是墙、木板和平面镜.手电筒的灯泡位于点G处,手电筒的光从平面镜上点B处反射后,恰好经过木板的边缘点F,落在墙上的点E处.点E到地面的高度ED=3.5 m,点F到地面的高度FC=1.5 m,灯泡到木板的水平距离AC=5.4 m,墙到木板的水平距离为CD=4 m.已知光在镜面反射中的入射角等于反射角,图中点A,B,C,D在同一水平面上,则灯泡到地面的高度GA为( )

A . 1.2 m
B . 1.3 m
C . 1.4 m
D . 1.5 m
-
9.
(2023九上·从江月考)
如图所示,在△ABC中,AB<AC,将△ABC以点A为中心逆时针旋转得到△ADE,点D在BC边上,DE交AC于点F.下列结论:①△AFE∽△DFC;②DA平分∠BDE;③∠CDF=∠BAD.其中正确的结论是( )

A . ①②
B . ②③
C . ①③
D . ①②③
-
10.
(2023九上·从江月考)
如图所示,在矩形ABCD中,AB=6,AD=4,点E,F分别为BC,CD的中点,BF,DE相交于点G,过点E作EH∥CD,交BF于点H,则线段GH的长度是( )

-
11.
(2023九上·从江月考)
如图所示,点E在矩形ABCD的AB边上,将△ADE沿DE翻折,点A恰好落在BC边上的点F处,若CD=3BF,BE=4,则AD的长为( )

A . 9
B . 12
C . 15
D . 18
-
12.
(2023九上·从江月考)
如图所示,在正方形ABCD中,E是BC的中点,F是CD上的一点,AE⊥EF,下列结论:①∠BAE=30°;②CE
2=AB·CF;③CF=

FD;④△ABE∽△AEF.其中正确的有( )

A . 1个
B . 2个
C . 3个
D . 4个
二、填空题:每小题4分,共16分.
-
13.
(2023九上·从江月考)
如图所示,在矩形ABCD中,E是边AB的中点,连接DE交对角线AC于点F,若AB=4,AD=3,则CF的长为
.

-
14.
(2023九上·从江月考)
如图所示,在△ABC中,点F,G在BC上,点E,H分别在AB,AC上,四边形EFGH是矩形,EH=2EF,AD是△ABC的高,BC=8,AD=6,那么EH的长为
.

-
15.
(2023九上·从江月考)
如图所示,Q为正方形ABCD的CD边上一点,CQ=1,DQ=2,P为BC上一点,若PQ⊥AQ,则CP=
.

-
16.
(2023九上·从江月考)
如图所示,小亮同学用自制的直角三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与树顶B在同一直线上.已知纸板的两条边EF=30 cm,DE=40 cm,延长DF交AB于点C,测得边DF离地面的高AC=1.5 m,CD=8 m,则树高AB等于
m.

三、解答题:本大题9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤.
-
-
-
-
(3)
在AB,BC,AC,DE,EF,DF这六条线段中,指出其中三组成比例的线段.
-
-
(1)
尺规作图:不写作法,保留作图痕迹.
①作∠ACB的平分线,交斜边AB于点D;
②过点D作BC的垂线,垂足为E.
-
-
-
20.
(2023九上·从江月考)
△ABC在平面直角坐标系内,三个顶点的坐标分别为A(0,3),B(3,4), C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).

-
(1)
画出△ABC向下平移4个单位长度得到的△A1B1C1 , 并且写出点C1的坐标;
-
(2)
以点B为位似中心,在网格内画出△A2B2C2 , 使△A2B2C2与△ABC位似,且相似比为2∶1,并写出点C2的坐标;
-
-
21.
(2023九上·从江月考)
如图所示,在正方形ABCD中,点E在边BC上(点E不与点B重合),连接AE,过点B作BF⊥AE于点F,交CD于点G.

-
-
-
22.
(2023九上·从江月考)
如图所示,AB∥FC,D是AB上一点,DF交AC于点E,DE=FE,分别延长FD和CB交于点G.

-
-
(2)
若GB=2,BC=4,BD=1,求AB的长.
-
23.
(2023九上·从江月考)
如图所示,在等腰三角形ABC中,AB=AC,点E,F在线段BC上,点Q在线段AB上,且CF=BE,AE
2=AQ·AB.

求证:
-
-
-
24.
(2023九上·从江月考)
如图所示,在Rt△ABC中,∠C=90°,AC=4 cm,BC=3 cm.动点M从点C出发,以1 cm/s的速度沿CA向终点A移动,同时动点P从点B出发,以2 cm/s的速度沿BA向终点A移动,连接PM,设移动时间为t s(0<t<2.5).求当t为何值时,以A,P,M为顶点的三角形与△ABC相似?

-
25.
(2023九上·从江月考)
小明想利用太阳光测量楼高.他带着皮尺来到一栋楼下,发现对面墙上有这栋楼的影子,针对这种情况,他设计了一种测量方案,具体测量情况如下:
如示意图,小明边移动边观察,发现站到点E处时,可以使自己落在墙上的影子与这栋楼落在墙上的影子重叠,且高度恰好相同.此时,测得小明落在墙上的影子高度CD=1.2 m,CE=0.8 m,CA=30 m(点A,E,C在同一直线上).已知小明的身高EF是1.7 m,请你帮小明求出楼AB的高度(结果精确到0.1 m).




















