一、单选题(本大题共10小题,每小题4分,满分40分)
-
A . 2.5
B . 10
C .  D .
D . 
-
-
-
4.
(2023八上·潜山月考)
为了测量被池塘隔开的A,B两点之间的距离,根据实际情况,作出如图所示图形,其中AB⊥BE,EF⊥BE,AF交BE于D,C在BD上.有四位同学分别测量出以下四组数据,根据所测数据不能求出A,B间距离的是( )
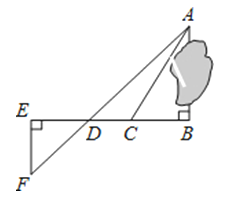
A . BC,∠ACB
B . DE,DC,BC
C . EF,DE,BD
D . CD,∠ACB,∠ADB
-
-
-
7.
(2023八上·潜山月考)
如果关于x的一元二次方程

有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”,下列说法:
①方程 是倍根方程;
是倍根方程;
②若 是倍根方程,则
是倍根方程,则 或
或 ;
;
③若方程 是倍根方程,且相异两点
是倍根方程,且相异两点 ,
,  都在抛物线
都在抛物线 上,则方程
上,则方程 的一个根为2.
的一个根为2.
其中,正确说法的个数是( )
-
8.
(2023八上·潜山月考)
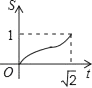
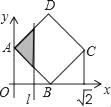
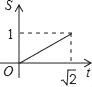
如图,正方形ABCD的顶点A(0,

),B(

,0),顶点C,D位于第一象限,直线x=t,(0≤t≤

),将正方形ABCD分成两部分,设位于直线l左侧部分(阴影部分)的面积为S,则函数S与t的图象大致是( )
-
9.
(2023八上·潜山月考)
如图

中,

,

为

中点,若点

为直线

下方一点,且

与

相似,则下列结论:①若

,

与

相交于

, 则点

不一定是

的重心;②若

, 则

的最大值为

;③若

, 则

的长为

;④若

, 则当

时,

取得最大值.其中正确的为( )

A . ①④
B . ②③
C . ①②④
D . ①③④
-
10.
(2023八上·潜山月考)
如图是由四个全等的三角形和一个正方形组成的大正方形,连结

与

交于

, 射线

交

于点

, 交

于点

, 交

于点

, 连接

, 则与

面积相等的图形是( )

二、填空题(本大题共4小题,每小题5分,满分20分)
-
-
-
13.
(2023八上·潜山月考)
已知抛物线

(
m为常数).若该抛物线与
x轴只有一个交点,则

;若该抛物线与直线

有两个不同的交点,且这两个交点都在抛物线对称轴的同侧,则
m的取值范围是
.
-
三、解答题(本大题共9小题,15、16、17、18每小题8分,19、20每小题10分,21、22每小题12分,23题14分,满分90分)
-
-
(1)
求

的值;
-
(2)
直接写出使一次函数值大于反比例函数值时x的取值范围.
-
-
17.
(2023八上·潜山月考)
如图,在矩形

中,边长

,

, 两动点

、

分别从

、

同时出发,点

从

沿

向

匀速运动,每秒

, 点

从

沿

向

匀速运动,每秒

, 两点

、

中有一点到达矩形的顶点则运动停止.设运动时间为

秒,

的面积为


-
-
-
(3)
当

取何值时,

的面积最大?并求出其最大面积.
-
18.
(2023八上·潜山月考)
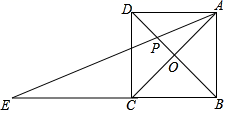
如图,正方形ABCD的边长为1,对角线AC、BD交于点O,E是BC延长线上一点,且AC=EC,连接AE交BD于点P.
-
-
-
19.
(2023八上·潜山月考)
某工厂加工一种产品的成本为30元/千克,根据市场调查发现,批发价定为48元/千克时,每天可销售500千克,为增大市场占有率,在保证盈利的情况下,工厂采取降价措施,批发价每千克降低1元,每天销量可增加50千克.
-
(1)
写出工厂每天的利润y元与降价x元之间的函数关系;
-
(2)
当降价多少元时,工厂每天的利润最大,最大为多少元?
-
(3)
当定价应设在什么范围之间时,可使工厂每天的利润要不低于9750元?
-
20.
(2023八上·潜山月考)
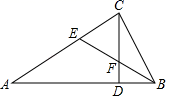
如图,在△ABC中,∠ACB=90°,CD是高,BE平分∠ABC.BE分别与AC,CD相交于点E,F.
-
-
-
21.
(2023八上·潜山月考)
如图所示,抛物线y=ax
2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.

-
-
(2)
小明在探究点D运动时发现,①当点D与点C重合时,EF长度可看作O;②当点D与点O重合时,EF长度也可以看作O,于是他猜想:设点D运动到OC中点位置时,当线段EF最长,你认为他猜想是否正确,为什么?
-
(3)
连接CF、DF,请直接写出△CDF为等腰三角形时所有t的值.
-
22.
(2023八上·潜山月考)
菱形ABCD中,F是对角线AC的中点,过点A作AE⊥BC垂足为E,G为线段AB上一点,连接GF并延长交直线BC于点H.

-
(1)
当∠CAE=30°时,且CE=

,求菱形的面积;
-
(2)
当∠BGF+∠BCF=180°,AE=BE时,求证:BF=(

+1)GF.
-
23.
(2023八上·潜山月考)
如图,抛物线y=ax
2+3x+c(a<0)与x轴交于点A和点B(点A在原点的左侧,点B在原点的右侧),与y轴交于点C,OB=OC=4.

-
-
(2)
如图1,连接BC,点D是直线BC上方抛物线上的点,连接OD,CD.OD交BC于点F,当S△COF:S△CDF=4:3时,求点D的坐标.
-
(3)
如图2,点E的坐标为(0,-2),点P是抛物线上的点,连接EB,PB,PE形成的△PBE中,是否存在点P,使∠PBE或∠PEB等于2∠OBE?若存在,请直接写出符合条件的点P的坐标;若不存在,请说明理由.
 B .
B .  C .
C .  D .
D . 

是倍根方程;
是倍根方程,则
或
;
是倍根方程,且相异两点
,
都在抛物线
上,则方程
的一个根为2.

 B .
B . 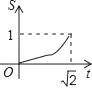 C .
C . 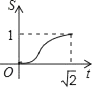 D .
D .