
求作:射线 , 使得
.
作法:①以点A为圆心,长为半径画圆;
②延长交
于点D , 以点D为圆心,
长为半径画弧,与
交于点P(点C , P在线段
的同侧);
③作射线 .
射线即为所求.
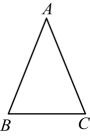
证明:连接 .
∵ ,
∴点C在上.
∵ ,
∴()(填推理依据).
∵ ,
∴.
∴ .
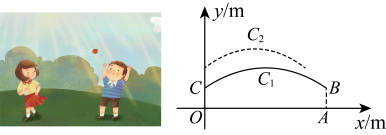
①依题意补全图形;
②直接写出和
的数量关系为 ▲ ;
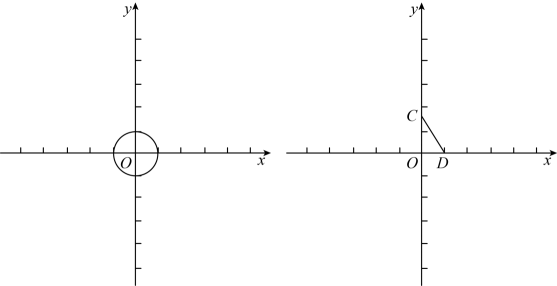
①在点 ,
,
中,是
的关联点的是 ▲ ;
②直线分别交x轴,y轴于点A , B , 若线段AB存在
的关联点,求b的取值范围;