浙江省嘉兴市重点中学2023-2024学年高三上学期数学1月...

更新时间：2024-04-16 浏览次数：60 类型：高考模拟

一、单项选择题：本题共8小题，每小题5分，共40分，在每小题给出的四个选项中，只有一项是符合要求的。

1. (2024高三上·嘉兴模拟) 已知复数 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . 0 B . 1 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024高三上·嘉兴模拟) 已知集合 $\text{[math]}$ ，则集合 $\text{[math]}$ 的元素个数为（）

A . 2 B . 3 C . 4 D . 5

答案解析收藏纠错 + 选题
3. (2024高三上·嘉兴模拟) 已知向量 $\text{[math]}$ ， $\text{[math]}$ ，若实数λ满足 $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . 1

答案解析收藏纠错 + 选题
4. (2024高三上·嘉兴模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则下列结论错误的为（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024高一上·桂林期末) 已知某物种 $\text{[math]}$ 年后的种群数量 $\text{[math]}$ 近似满足函数模型： $\text{[math]}$ （ $\text{[math]}$ ，当 $\text{[math]}$ 时表示2023年初的种群数量）.自2023年初起，经过 $\text{[math]}$ 年后 $\text{[math]}$ ，当该物种的种群数量不足2023年初的 $\text{[math]}$ 时， $\text{[math]}$ 的最小值为（参考数据： $\text{[math]}$ ）（）

A . 16 B . 17 C . 18 D . 19

答案解析收藏纠错 + 选题
6. (2024高三上·慈溪期末) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ，令 $\text{[math]}$ ．若数列 $\text{[math]}$ 是公比为2的等比数列，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024高三上·嘉兴模拟) 正四面体的棱长为 $\text{[math]}$ ，点 $\text{[math]}$ ， $\text{[math]}$ 是它内切球球面上的两点， $\text{[math]}$ 为正四面体表面上的动点，当线段 $\text{[math]}$ 最长时， $\text{[math]}$ 的最大值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024高三上·嘉兴模拟) 已知椭圆 $\text{[math]}$ 的左、右焦点分别为 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为椭圆上不与左右顶点重合的任意一点， $\text{[math]}$ ， $\text{[math]}$ 分别为 $\text{[math]}$ 的内心和重心，当 $\text{[math]}$ 轴时，椭圆的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、 多项选择题：本题共4小题，每小题5分，共20分，在每小题给出的四个选项中，有多项符合题目的要求，全部选对的得5分，部分选对的得2分，有选错的得0分。

9. (2024高三上·嘉兴模拟) 下列说法正确的是（）

A . 正切函数是周期函数，最小正周期为π B . 正切函数的图象是不连续的 C . 直线 $\text{[math]}$ 是正切曲线的渐近线 D . 把 $\text{[math]}$ 的图象向左、右平行移动 $\text{[math]}$ 个单位，就得到 $\text{[math]}$ $\text{[math]}$ 的图象

答案解析收藏纠错 + 选题
10. (2024高三上·嘉兴模拟) 下列说法正确的是（）

A . 事件A与事件B互斥，则它们的对立事件也互斥． B . 若 $\text{[math]}$ ，且 $\text{[math]}$ ，则事件A与事件B不是独立事件． C . 若事件A ， B ， C两两独立，则 $\text{[math]}$ ． D . 从2个红球和2个白球中任取两个球，记事件 $\text{[math]}$ {取出的两个球均为红色}， $\text{[math]}$ {取出的两个球颜色不同}，则A与B互斥而不对立．

答案解析收藏纠错 + 选题
11. (2024高三上·汕尾期末) 已知抛物线 $\text{[math]}$ 的焦点为 $\text{[math]}$ ，经过点 $\text{[math]}$ 的直线l与C交于A ， B两点，且抛物线C在A ， B两点处的切线交于点P ， D为AB的中点，直线PD交C于点E ，则（）

A . 点P在直线 $\text{[math]}$ 上 B . E是PD的中点 C . $\text{[math]}$ D . $\text{[math]}$ 轴

答案解析收藏纠错 + 选题
12. (2024高三上·嘉兴模拟) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . 当 $\text{[math]}$ 时， $\text{[math]}$ 有2个零点 B . 当 $\text{[math]}$ 时， $\text{[math]}$ 有2个零点 C . 存在 $\text{[math]}$ ，使得 $\text{[math]}$ 有3个零点 D . 存在 $\text{[math]}$ ，使得 $\text{[math]}$ 有5个零点

答案解析收藏纠错 + 选题

三、填空题：本题共4小题，每小题5分，共20分。

13. (2024高三上·嘉兴模拟) $\text{[math]}$ 展开式中的常数项是120，则实数 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2024高三上·嘉兴模拟) 若数列 $\text{[math]}$ 满足 $\text{[math]}$ ，则 $\text{[math]}$ .

答案解析收藏纠错 + 选题
15. (2024高三上·嘉兴模拟) 半径为R的球的内接正三棱柱的侧面积（各侧面面积之和）的最大值为．

答案解析收藏纠错 + 选题
16. (2024高三上·嘉兴模拟) 对任意 $\text{[math]}$ ，函数 $\text{[math]}$ 恒成立，则a的取值范围为．

答案解析收藏纠错 + 选题

四、 解答题：本题共6小题，共70分，解答应写出必要的文字说明、证明过程及验算步骤。

17. (2024高三上·嘉兴模拟) 已知在等差数列 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和，且满足 $\text{[math]}$ .
1. （1）求数列 $\text{[math]}$ 和 $\text{[math]}$ 的通项公式；
2. （2）设 $\text{[math]}$ $\text{[math]}$ ，求数列 $\text{[math]}$ 的前 $\text{[math]}$ 项和 $\text{[math]}$ .
答案解析收藏纠错 + 选题
18. (2024高三上·贵州模拟) 在 $\text{[math]}$ 中，内角A ， B ， C的对边分别为a ， b ， c ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）求角A；
2. （2）作角A的平分线与 $\text{[math]}$ 交于点 $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ .
答案解析收藏纠错 + 选题
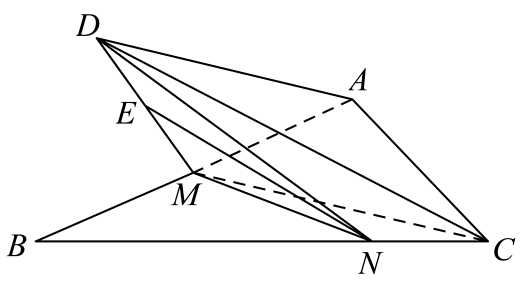
19. (2024高三上·嘉兴模拟) 如图所示，已知 $\text{[math]}$ 是以 $\text{[math]}$ 为斜边的等腰直角三角形，点 $\text{[math]}$ 是边 $\text{[math]}$ 的中点，点 $\text{[math]}$ 在边 $\text{[math]}$ 上，且 $\text{[math]}$ ．以 $\text{[math]}$ 为折痕将 $\text{[math]}$ 折起，使点 $\text{[math]}$ 到达点 $\text{[math]}$ 的位置，且平面 $\text{[math]}$ 平面 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）若 $\text{[math]}$ 是线段 $\text{[math]}$ 的中点，求证： $\text{[math]}$ 平面 $\text{[math]}$ ；
2. （2）求二面角 $\text{[math]}$ 的余弦值．
答案解析收藏纠错 + 选题
20. (2024高三上·嘉兴模拟) 为了避免就餐聚集和减少排队时间，某校食堂从开学第1天起，每餐只推出即点即取的米饭套餐和面食套餐.某同学每天中午都会在食堂提供的两种套餐中选择一种套餐，如果他第1天选择了米饭套餐，那么第2天选择米饭套餐的概率为 $\text{[math]}$ ；如果他第1天选择了面食套餐，那么第2天选择米饭套餐的概率为 $\text{[math]}$ .已知他开学第1天中午选择米饭套餐的概率为 $\text{[math]}$ .
1. （1）求该同学开学第2天中午选择米饭套餐的概率；
2. （2）记该同学第 $\text{[math]}$ 天选择米饭套餐的概率为 $\text{[math]}$ ，
  （i）证明： $\text{[math]}$ 为等比数列；
  （ii）证明：当 $\text{[math]}$ 时， $\text{[math]}$ .
答案解析收藏纠错 + 选题
21. (2024高三上·嘉兴模拟) 已知 $\text{[math]}$ 为双曲线 $\text{[math]}$ 上异于左、右顶点的一个动点，双曲线 $\text{[math]}$ 的左、右焦点分别为 $\text{[math]}$ ，且 $\text{[math]}$ ．当 $\text{[math]}$ 时， $\text{[math]}$ 的最小内角为 $\text{[math]}$ ．
1. （1）求双曲线 $\text{[math]}$ 的标准方程．
2. （2）连接 $\text{[math]}$ ，交双曲线于另一点 $\text{[math]}$ ，连接 $\text{[math]}$ ，交双曲线于另一点 $\text{[math]}$ ，若 $\text{[math]}$ ．
  ①求证： $\text{[math]}$ 为定值；
  ②若直线AB的斜率为−1，求点P的坐标．
答案解析收藏纠错 + 选题
22. (2024高三上·嘉兴模拟) 函数 $\text{[math]}$ .
1. （1）求函数 $\text{[math]}$ 的单调增区间；
2. （2）当 $\text{[math]}$ 时，若 $\text{[math]}$ ，求证： $\text{[math]}$ ；
3. （3）求证：对于任意 $\text{[math]}$ 都有 $\text{[math]}$ .
答案解析收藏纠错 + 选题