备战2024年中考数学细点逐一突破真题训练第5章不等式（组）...

更新时间：2024-03-04 浏览次数：83 类型：一轮复习

一、不等式性质

1. (2024七上·大兴期末) 如图，数轴上的点 $\text{[math]}$ 表示的数分别是 $\text{[math]}$ ．如果 $\text{[math]}$ ，且 $\text{[math]}$ ，那么该数轴的原点 $\text{[math]}$ 的位置应该在（）

A . 点 $\text{[math]}$ 的左侧 B . 点 $\text{[math]}$ 的右侧 C . 点 $\text{[math]}$ 与点 $\text{[math]}$ 之间且靠近点 $\text{[math]}$ D . 点 $\text{[math]}$ 与点 $\text{[math]}$ 之间且靠近点 $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八上·邵阳期末) 已知关于x的不等式（a﹣1）x＞2的解集为 $\text{[math]}$ ，则a的取值范围是（）

A . a＜1 B . a＞1 C . a＜0 D . a＞0

答案解析收藏纠错 + 选题
3. (2024七下·静宁期末) 下列说法不一定成立的是（）

A . 若a>b，则a+c>b+c B . 若a+c>b+c，则a>b C . 若a>b，则ac²>bc² D . 若ac²>bc² ，则a>b

答案解析收藏纠错 + 选题
4. (2023·高明模拟) 已知 $\text{[math]}$ ，下列选项正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2023·安庆模拟) 已知实数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 满足 $\text{[math]}$ ， $\text{[math]}$ ，则下列选项中正确的（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题

二、不等式（组）及其解集

6. (2024八上·邵阳期末) 疫情期间，有一批患者要入住邵阳市中心医院的某栋大楼，若每间住4人，则有38人无法入住；若每间住5人，则最后一间没住满．若设房间数为x间，则可列不等式组为：．

答案解析收藏纠错 + 选题
7. (2023·汉中模拟) 解不等式（组）：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
8. (2023八上·杭州月考) 已知关于x的不等式组 $\text{[math]}$ 的整数解共有4个，则a的取值范围是（）

A . ﹣3＜a≤﹣2 B . ﹣3≤a＜﹣2 C . ﹣3＜a＜﹣2 D . a＜﹣2

答案解析收藏纠错 + 选题
9. 已知不等式组 $\text{[math]}$ 的解集是 $\text{[math]}$ ，则 $\text{[math]}$ =（）

A . 0 B . -1 C . 1 D . 2023

答案解析收藏纠错 + 选题
10. (2023八上·义乌期中) 用锤子以相同的力将铁钉垂直钉入木块，随着铁钉的深入，铁钉所受的阻力也越来越大．当铁钉未进入木块部分长度足够时，每次钉入木块的铁钉长度是前一次的 $\text{[math]}$ ，已知这个铁钉被敲击3次后全部进入木块（木块足够厚），且第一次敲击后，铁钉进入木块的长度是acm，若铁钉总长度为6cm，则a的取值范围是．

答案解析收藏纠错 + 选题
11. (2024九下·渝北开学考) 若整数 $\text{[math]}$ 使得关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 有解，且使得关于 $\text{[math]}$ 的分式方程 $\text{[math]}$ 有正整数解，那么符合条件的所有整数 $\text{[math]}$ 的和为．

答案解析收藏纠错 + 选题
12. (2024八下·新化开学考) 对于三个数a ， b ， c ，我们规定 $\text{[math]}$ 表示这三个数中最大的数.例如 $\text{[math]}$ ， $\text{[math]}$ 若 $\text{[math]}$ ，则x的取值范围是．

答案解析收藏纠错 + 选题

三、不等式（组）的特殊解

13. (2024九下·合肥模拟) 不等式 $\text{[math]}$ 的正整数解有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
14. (2024九下·牙克石模拟) 若关于x的分式方程 $\text{[math]}$ 的解为非负数，则m的取值范围是（）

A . $\text{[math]}$ 且 $\text{[math]}$ B . $\text{[math]}$ 且 $\text{[math]}$ C . $\text{[math]}$ 且 $\text{[math]}$ D . $\text{[math]}$ 且 $\text{[math]}$

答案解析收藏纠错 + 选题
15. (2023八上·东安月考) 若不等式组 $\text{[math]}$ 有解，则 $\text{[math]}$ 的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
16. (2023九上·渝北期中) 若整数 $\text{[math]}$ 使得关于 $\text{[math]}$ 的分式方程 $\text{[math]}$ 有正整数解，且使关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ 至少有 $\text{[math]}$ 个整数解，那么符合条件的所有整数 $\text{[math]}$ 的和为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2023·曹县模拟) 关于x，y的方程组 $\text{[math]}$ 的解中，x与y的和不大于3，则k的取值范围是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
18. 若关于x的不等式组 $\text{[math]}$ 的解为x<-2，且关于y的分式方程 $\text{[math]}$ 的解为正数，则所有满足条件的整数a的值之和为.

答案解析收藏纠错 + 选题

四、函数与不等式结合

19. (2024八上·杭州期末) 如图，一次函数y₁＝kx+b与y₂＝mx+n的图象相交于点（1，3），则方程组 $\text{[math]}$ 的解为 $\text{[math]}$ ，关于x的不等式kx+b＞mx+n的解为．

答案解析收藏纠错 + 选题
20. (2023九上·中江期中) 如图，已知二次函数y₁₌ $\text{[math]}$ 的图象与正比例函数y₂＝kx（k≠0）的图象相交于点A（3，4），与x轴交于点B（2，0），若0＜y₁＜y₂ ，则x的取值范围是（　　）

A . $\text{[math]}$ B . 2＜x＜3 C . $\text{[math]}$ D . 0＜x＜3

答案解析收藏纠错 + 选题
21. (2024八上·杭州期末) 已知一次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ．则对于不等式 $\text{[math]}$ ，下列说法正确的是（）

A . 当 $\text{[math]}$ 时， $\text{[math]}$ B . 当 $\text{[math]}$ 时， $\text{[math]}$ C . 当 $\text{[math]}$ 且 $\text{[math]}$ 时， $\text{[math]}$ D . 当 $\text{[math]}$ 且 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题
22. (2023·静安模拟) 已知反比例函数 $\text{[math]}$ 的图像经过点 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的值；
2. （2）完成下面的解答过程．
  解不等式组 $\text{[math]}$
  
  解：解不等式①，得；
  
  在方格中画出反比例函数 $\text{[math]}$ 的大致图像，根据图像写出不等式②的解集是；
  
  把不等式①和②的解集在数轴上表示出来；
  
  从图中可以找出这两个不等式解集的公共部分，得到原不等式组的解集是．
答案解析收藏纠错 + 选题
23. (2024九上·扶余期末) 自主学习，请阅读下列解题过程．
解一元二次不等式： $\text{[math]}$ ＞0．
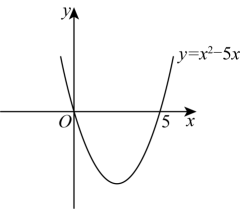
解：设 $\text{[math]}$ =0，解得： $\text{[math]}$ =0， $\text{[math]}$ =5，则抛物线y= $\text{[math]}$ 与x轴的交点坐标为（0，0）和（5，0）．画出二次函数y= $\text{[math]}$ 的大致图象（如图所示），由图象可知：当x＜0，或x＞5时函数图象位于x轴上方，此时y＞0，即 $\text{[math]}$ ＞0，所以，一元二次不等式 $\text{[math]}$ ＞0的解集为：x＜0或x＞5．
通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：
1. （1）上述解题过程中，渗透了下列数学思想中的和．（只填序号）
  ①转化思想 ②分类讨论思想 ③数形结合思想
2. （2）一元二次不等式 $\text{[math]}$ ＜0的解集为．
3. （3）用类似的方法解一元二次不等式： $\text{[math]}$ ＞0．
答案解析收藏纠错 + 选题

五、一次不等式的实际应用

24. (2024八上·讷河期末) 综合与实践问题情境：“文房四宝”是中国独有的书法绘画工具，即笔、墨、纸、砚，文房四宝之名，起源于南北朝时期．某中学为了落实双减政策，丰富学生的课后服务活动，开设了书法社团，计划为学生购买A，B两种型号“文房四宝”共40套．已知某文化用品店每套A型号的“文房四宝”的标价比B型号的“文房四宝”的标价高30%，若按标价购买需花费4300元，其中购买B型号“文房四宝”花费3000元．
问题解决：
1. （1）求每套B型号的“文房四宝”的标价．
2. （2）若经过与店主协商，考虑到购买较多，店主同意该中学按A型号“文房四宝”九折，B型号“文房四宝”八折的优惠价购入，则购买原定数量的A，B型号“文房四宝”共需花费多少元？
3. （3）一段时间后，由于传统文化广受关注，另一所学校想要购入A，B两种型号“文房四宝”共100套。店主继续以（2）中的折扣价进行销售，已知A，B两种型号的“文房四宝”每套进价分别为67元和50元，若通过此单生意，该店主获利不低于3800元，则该校在这家店至少买了套A型“文房四宝”？
答案解析收藏纠错 + 选题
25. (2024八上·浑江期末) 某企业有甲、乙两个车间用于生产医用防护服.甲车间每天生产的数量是乙车间每天生产数量的1.5倍，两车间各加工6000套医用防护服，甲车间比乙车间少用4天.
1. （1）甲、乙两车间每天各生产多少套医用防护服？
2. （2）已知甲、乙两车间生产这种医用防护服每天的生产费用分别是12000元和10000元，现有18000套医用防护服的生产任务，甲车间单独生产一段时间后另有安排，剩余任务由乙车间单独完成.如果总生产费用不超过339000元，则甲车间至少需要生产几天？
答案解析收藏纠错 + 选题
26. (2023九上·怀仁月考) 某公园要铺设广场地面，其图案设计如图所示．矩形地面的长为50米，宽为32米，中心建设一个直径为10米的圆形喷泉，四周各角留一个相同的矩形花坛，图中阴影处铺设地砖．已知矩形花坛的长比宽多15米，铺设地砖的面积是1125平方米．（ $\text{[math]}$ 取3）
1. （1）求矩形花坛的宽是多少米；
2. （2）四个角的矩形花坛由甲、乙两个工程队负责绿化种植，甲工程队每平方米施工费为100元，乙工程队每平方米施工费为120元．若完成此工程的工程款不超过42000元，至少要安排甲队施工多少平方米？
答案解析收藏纠错 + 选题

六、方程组与不等式结合

27. (2024八上·防城期末) 【综合与实践】
学校在某商场购买甲、乙两种不同类型的足球，相关信息如下：购买甲种足球共用2000元，购买乙种足球共花费1400元.已知购买一个乙种足球比购买一个甲种足球多花20元.设购买一个甲种足球的单价是 $\text{[math]}$ 元。
1. （1）请用含 $\text{[math]}$ 的代数式分别表示购买甲、乙两种足球的数量；
2. （2）若本次购买甲种足球的数量是购买乙种足球数量的2倍，求甲、乙两种足球在此商场的销售单价；
3. （3）为满足学生需求，这所学校决定再次购买甲、乙两种足球共50个.恰逢该商场对两种足球的销售单价进行调整，甲种足球的销售单价比上次购买时提高了10％，乙种足球的销售单价比上次购买时降低了10％.如果此次购买甲、乙两种足球的总费用不超过2950元，求这所学校最多可以购买乙种足球的数量.
答案解析收藏纠错 + 选题
28. (2023八上·南宁开学考) 某商场“双 $\text{[math]}$ ”前准备从供货商家处新选购一批商品，已知按进价购进 $\text{[math]}$ 件甲种商品和 $\text{[math]}$ 件乙种商品共需 $\text{[math]}$ 元，购进 $\text{[math]}$ 件甲种商品和 $\text{[math]}$ 件乙种商品共需 $\text{[math]}$ 元．
1. （1）求甲、乙两种商品每件的进价分别是多少元？
2. （2）若甲种商品的售价为每件 $\text{[math]}$ 元，乙种商品的售价为每件 $\text{[math]}$ 元，该商场准备购进甲、乙两种商品共 $\text{[math]}$ 件，且这两种商品全部售出后总利润不少于 $\text{[math]}$ 元，不高于 $\text{[math]}$ 元．若购进甲种商品 $\text{[math]}$ 件，请问该商场共有哪几种进货方案？
3. （3）根据往年销售情况，商场计划在“双 $\text{[math]}$ ”当天将现有的甲、乙两种商品共 $\text{[math]}$ 件按 $\text{[math]}$ 中的售价全部售完．但因受拉尼娜现象形成的冷空气持续影响，当天出现的雨雪天气使得 $\text{[math]}$ 件商品没有全部售完，两种商品的实际销售利润总和为 $\text{[math]}$ 元．那么，“双 $\text{[math]}$ ”当天商场至少卖出乙种商品多少件？
答案解析收藏纠错 + 选题

29. (2023八下·江岸期末) 为了迎接“十·一”小长假的购物高峰．某运动品牌专卖店准备购进甲、乙两种运动鞋．其中甲、乙两种运动鞋的进价和售价如下表：

运动鞋价格/种类	甲	乙
进价（元/双）	m	$\text{[math]}$
售价（元/双）	160	120

已知：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同．

（1）求m的值；
（2）要使购进的甲、乙两种运动鞋共200双的总利润（利润 $\text{[math]}$ 售价 $\text{[math]}$ 进价）不少于10800元，且不超过11100元，问该专卖店有几种进货方案？
（3）在（2）的条件下，专卖店准备对甲种运动鞋进行优惠促销活动，决定对甲种运动鞋每双优惠 $\text{[math]}$ 元出售．乙种运动鞋价格不变．那么该专卖店要获得最大利润应如何进货？

答案解析收藏纠错 + 选题

七、实践探究题

30. (2023·舟山模拟) 观察： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）猜想：当 $\text{[math]}$ 时， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ （“>”“＝”“<”填空）
2. （2）探究：当 $\text{[math]}$ 时， $\text{[math]}$ 与 $\text{[math]}$ （其中n为正整数）的大小关系，并说明理由．
答案解析收藏纠错 + 选题
31. (2023·龙岗模拟) 对于“已知 $\text{[math]}$ ，求 $\text{[math]}$ 的最大值”这个问题，小明是这样求解的：
∵ $\text{[math]}$ ， ∴ $\text{[math]}$ ， ∴ $\text{[math]}$
∴ $\text{[math]}$ ，所以 $\text{[math]}$ 的最大值为 $\text{[math]}$ .
请你按照这种方法计算：当 $\text{[math]}$ 时， $\text{[math]}$ 的最小值.

答案解析收藏纠错 + 选题